Have ideas? Tell me.
the best layout
Partially optimized QWKRFY and fully optimized QGMLWY layouts are the last word in easier typing.
the worst layout
A fully anti-optimized TNWMLC layout is a joke and a nightmare. It's also the only keyboard layout that has its own fashion line.
download and explore
Download keyboard layouts, or run the code yourself to explore new layouts. Carpalx is licensed under CC BY-NC-SA 4.0.
layouts
Download and install the layouts.
Component Optimization
ON THIS PAGE
Purpose of Individual Component Optimization
Combined Base and Stroke Path Optimization
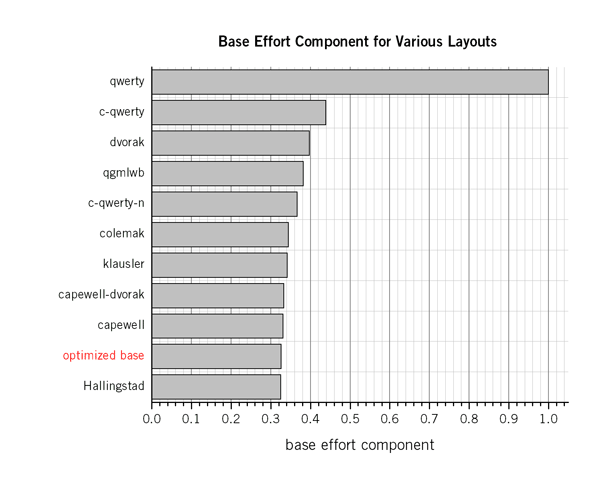
The Carpalx typing model is composed of three components: base effort, penalties and stroke path. This section explores the layouts that result when individual components are minimized. The section explains how to go about finding a layout that has uniformly better effort statistics than a popular alternative, such as Colemak.
Purpose of Individual Component Optimization
The typing effort model models effort as a sum of three distinct components: base (finger distance), penalty (row and finger penalties) and stroke (finger and hand progression). The optimized layouts presented thus far were generated by minimizing the sum of these individual components, which were weighted in a 1:1:1 ratio.
I initially chose this ratio because it is easily justifable &mdash it does not favour any one effort component. In this section, as I explore the properties of individual effort components, you'll see that it makes sense to adjust this ratio. In fact, when the ratio is adjusted to 10:1:10 another family of layouts that compete directly with Colemak is generated.
WHAT COMPONENT IS IMPORTANT TO YOU? Each component in the effort model is designed to measure different aspects of a layout. The base effort component is strictly a function of finger travel distance. Thus, if your only concern is having as short a finger travel distance as possible, this is the critical component. The penalty component is meant to penalize the use of off-home rows and certain fingers (e.g ring and pinky). If you prefer to limit the use of the pinky, then the penalty component should be given sufficient enough weight to transfer the effort to other fingers. Finally, the stroke effort measures hand and finger alternation, row jumping and finger rolling. The purpose of this component is to capture desirable layout characteristics that are would otherwise not be identified by either the base or penalty components.
Beyond a point, it is not possible to improve all three individual components. For example, if you seek a lower penalty, you would choose a layout that makes less use of the pinky. However, this transfers more work to the other fingers and increases the finger repetition frequency, which in turn increases the stroke path. In another example, if you want to limit the finger travel distance, you would limit the use of T and Y keys, but this means transfering more work to other fingers and similarly increasing the stroke path and (possibly) the penalty, if the ring finger and pinky get more work.
Ultimately, you should use the individual effort component values to determine the strengths of a given layout. In addition, the detailed hand, finger and row frequency statistics will provide additional information (hand asymmetry, finger frequencies, etc) that is not conveyed in the effort components.
In each part of this section, I ask the following: "What kind of layouts result when each of the components is minimized individually?" For example, what is the layout (or as we'll see, what family of layouts) has the lowest base effort? Another useful question would be, "What happens to the penalty of a layout as base effort is minimized."
All the optimizations described in this section use a modified QWERTY initial state, where the ; and P were swapped. Colemak uses this character mask, and it's a good one because it makes better use of home row.

component weight adjustments
To minimize individual effort components, the effort component weights for base, effort and stroke path (kb, kp, ks) were adjusted as follows. Given a component to minimize (e.g. base), all other weights (e.g. effort and stroke path) were set to zero. Next, the effort weight was adjusted so that the total effort for QWERTY with the adjusted parameter would be 3.000. This adjustment was done so that the final effort found in this section could be compared directly to the efforts of QWERTY and other layouts reported in other sections.
Specifically, the parameters were: base minimization (kb=1.0665, kp=ks), penalty minimization (kp=1.9269, kb=ks), stroke path minimization (ks=1.2804, kb=kp), base+penalty minimization (kb=0.5333, kp=0.9634, ks=0), and base+stroke minimization (kb=0.5333, ks=0.6402, kp=0).
Base Effort Optimization
In this section, I present the family of layouts (very large family, in fact) which have the minimum base effort. As it turns out, minimizing the base effort component does not yield a unique solution.
Recall that the base effort is a function of finger distance only — it is insufficiently constrained to ensure a unique solution. This is reasonable to expect, because most keys are equidistant from home row and, in the absence of other constraints, the solutions are symmetric with respect to equidistant keys. Minimum effort is easily achieved (1286/1600 runs of the minimization process generated a minimum effort layout). These layouts are presented below, with keys annotated with letters according to their frequency in the layouts.
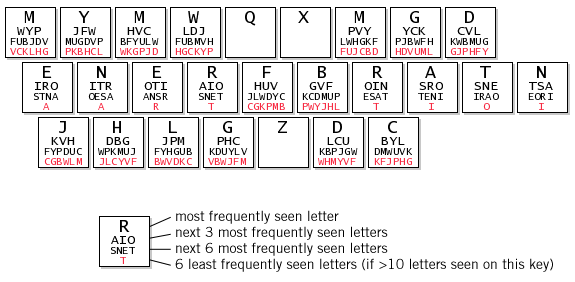
Note that Q, X and Z are uniquely positioned during the minimization. It is not surprising that the home row keys are assigned fewer letters in the optimal solution set than other rows, since frequently used letters are naturally assigned to home row.
The lowest base effort seen out of all the layouts was Hallingstad (0.325) which is marginally lower than the minimized base effort of 0.326 seen here. Hallingstad's extremely low base effort is a result of its very unusual layout, which relocates additional punctuation keys, such as the comma, apostrophe, semicolon and period. Importantly, both the T and Y keys which have large finger travel distance, and which are use for letters in other layouts, are used for punctuation in Hallingstad's layout (' and ;).
Figure 3 suggests that there is significant room for improvement in the base component. A very large number of layouts nearly match (0.326 vs 0.325) Hallingstand's Arensito layout. It is reasonable to expect that within the family of layouts that minimize the base effort, some will have favourable penalty and stroke components. I explore this below.
penalty and stroke values for minimum base effort solutions
By minimizing one component (e.g. base effort), the other two components (e.g. penalty and stroke) are unconstrained. Because a large number of layouts minimizes the base effort, we expect a distribution of penalty and stroke components within these layouts. This range of penalty and stroke path efforts for the minimal base effort solutions is plotted below.
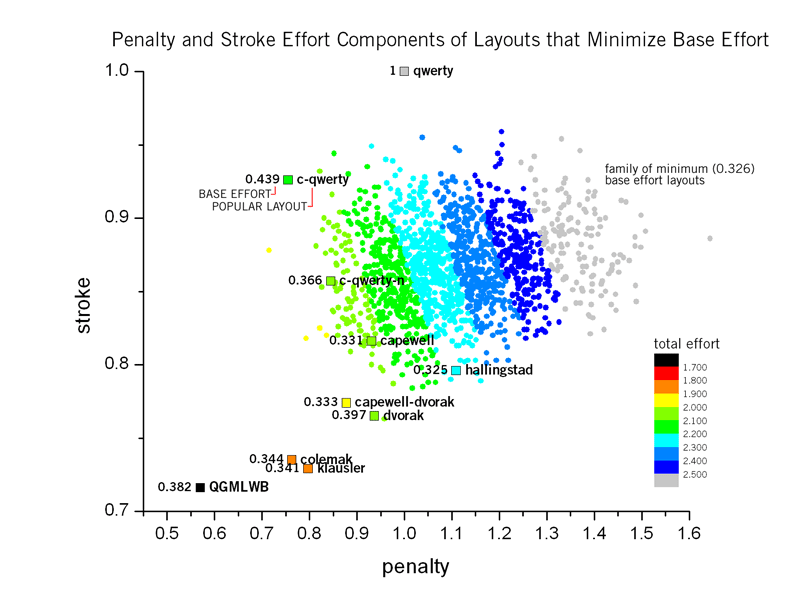
The family of solutions ranges has a penalty range of 0.715-1.644 and a stroke path range of 0.763-0.959. Certain popular alternative layouts like Capewell, c-qwerty-n and Hallingstad lie within the distribution of solutions. In other words, there are solutions that have improve all three components with respect to these layouts. There is a solution very close to Dvorak (slightly higher penalty than Dvorak). Capewell-Dvorak has both a low penalty and stroke value and there aren't any nearby solutions.
Layouts such as Colemak and Klausler have significantly lower penalty and stroke values than all the members of the minimum base effort solution set. These two layouts sacrifice their base component (which is about 5% higher than the lowest possible), in favour of decreasing their penalty and stroke component. In other words, finger travel distance isn't the only motivating factor behind Colemak and Klausler and any process whose purpose is to solely minimize finger distance will not sample the family of layouts with Colemak-like properties.
In conclusion, focus on solely optimizing the base effort component alone has limited usefulness. Although the final layout will have the lowest finger travel distance — you'll be on home row most of the time — other aspects of the layout (frequent use of the pinky, finger repetition) will reduce its desirability. Thus, looking ahead, to explore Colemak-like layouts it will be helpful to eventually minimize the base and stroke components and either eliminate the penalty component, or lower its weight.
Penalty Optimization
When only the penalty component of effort is minimized, another family of layout solutions is obtained. Recall that the penalty component increases effort based on hand, row and finger usage. For example, each time the pinky and ring fingers are used, a penalty is incurred.
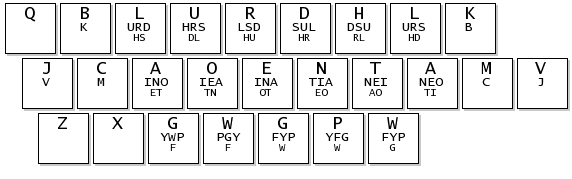
The result of optimizing the penalty component is a layout family that focuses all the frequently used keys on home row and within service distance of the fingers that do not incur a penalty (middle and index). Infrequently used letters are pushed to the corners of the layout — there is no ambiguity in where Q, Z, and X are placed, which is, in fact, the same locations as in QWERTY.
The penalty component is the least appropriate component to be used exclusively. It is incorporated into the model to allow balancing of finger and row and is insufficiently parametrized to act as the sole guiding force towards a good layout. Because it is not sensitive to finger distance (beyond row-based penalties), certain keys such as F/G and are symmetric. Clearly, any model should not not treat these fingers, since G involves lateral finger movement while F does not.
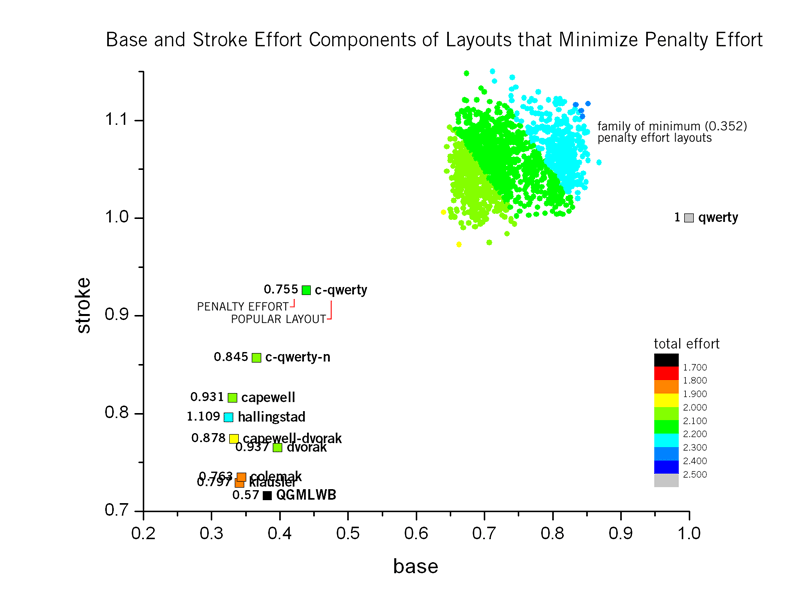
As the figure above shows, the minimum penalty solution set is quite tightly grouped in base/stroke effort space (78 optimal solutions were found, out of 1600 runs; compare this to 1286/1600 for base effort optimization). From the figure above you can see that, although the penalty has been minimized, base and stroke effort components are much higher for these layouts than nearly all other alternatives. Only QWERTY has a higher base component. The distance between the solution cluster and all the layout alternatives emphasizes that the penalty component cannot be used by itself. It also suggests that layout properties that minimize the penalty component generate a large increase in base and stroke components and that, therefore, the penalty component should be weighted carefully if low base and stroke effort components are sought.
The lowest achievable penalty component effort is 0.352. This is a significant decrease (38%) from the next-best layout (with respect to penalty), which is the fully optimized QGMLWB layout. But, as Figure 6 shows, this decrease comes at a cost of significantly increase stroke and base efforts.
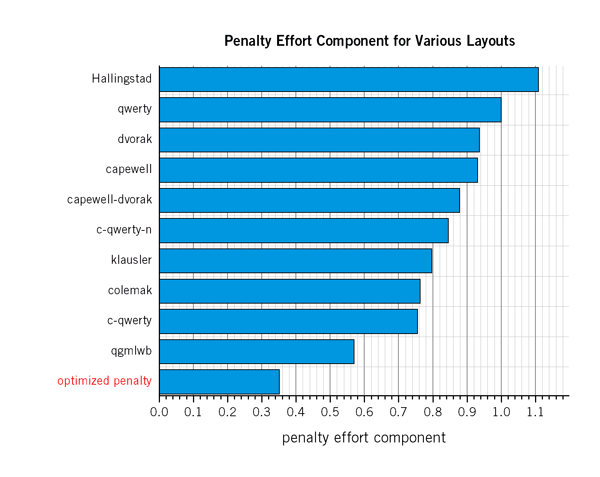
In fact, if you compare Figure 3 to Figure 7, it is clear that after full optimization (e.g. QGMLWB) there remains room for improvement in the penalty component. The optimization does not take advantage of this potential improvement because doing so would drastically increase other effort components.
Stroke Path Optimization
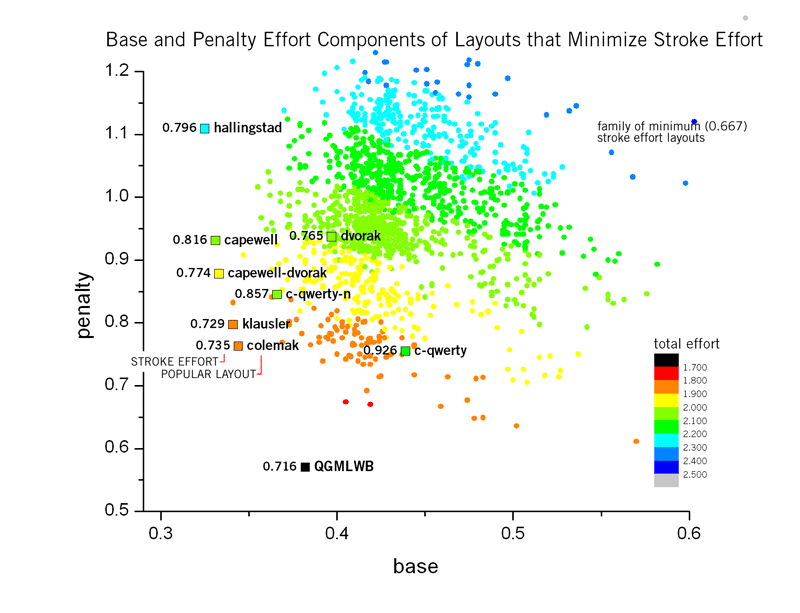
The final component effort that can be studied individually is the stroke path component. This is the most complex of all the efforts and, therefore, it is not surprising that minimizing it results in the smallest set of solutions. In fact, out of 1600 simulation runs, only 5 minimal solutions were found, with other solutions ranging in stroke effort from 0.667-0.735.

Layouts with a low stroke effort are those where hand and finger alternation is increased, keys are typed in a rolling motion of the fingers, and row jumps between successive key strokes is decreased.
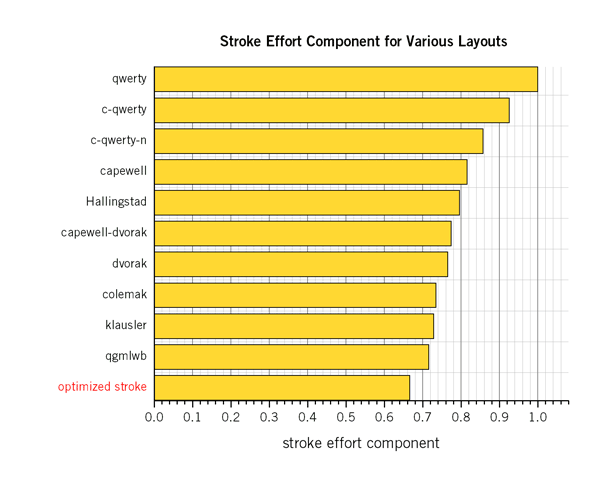
The figure above demonstrates that the stroke component is one in which the least improvement can be made over QWERTY. While the lowest base and penalty efforts were 0.326 and 0.352, respectively, the lowest stroke effort that can be achieved is 0.667 (compare these to QWERTY which has 1.000 for each component).
Solutions to minimizing stroke effort, as shown in the figure below, come close in base and penalty scores to popular alternatives. However, no solutions improve both base and penalty components of Hallingstad, Capewell, Capewell-Dvorak, Klausler or Colemak. While solutions exist that improve both stroke and penalty, this is at the cost of a higher base component.
Combined Base and Stroke Path Optimization
Figures 4 and 10 suggest that the base and stroke path components are practically useful measures of effort. When these are optimized, the effort characteristics of the solution set approaches that of popular layouts. Therefore, in this section I examine the layouts created when both base and stroke path are optimized simulataneously. The base, stroke and penalty weights for this simulation are kb=0.5333, ks=0.6402, kp=0.
The plot below shows the simulation results for optimization base+stroke path components. As before, to optimize one quantity (base+stroke), another quantity (penalty) is increased. The minimum base+effort layout found (total 1.018) has a relatively high penalty of 1.059 (higher than QWERTY). A couple of low-penalty layouts in the solution set are annotated in the figure, but neither have all three effort components lower than Colemak. For example, YBUFPQ has a lower base (0.332 vs 0.344) and stroke (0.734 vs 0.735) components than Colemak, but a higher penalty 0.786 vs 0.763.
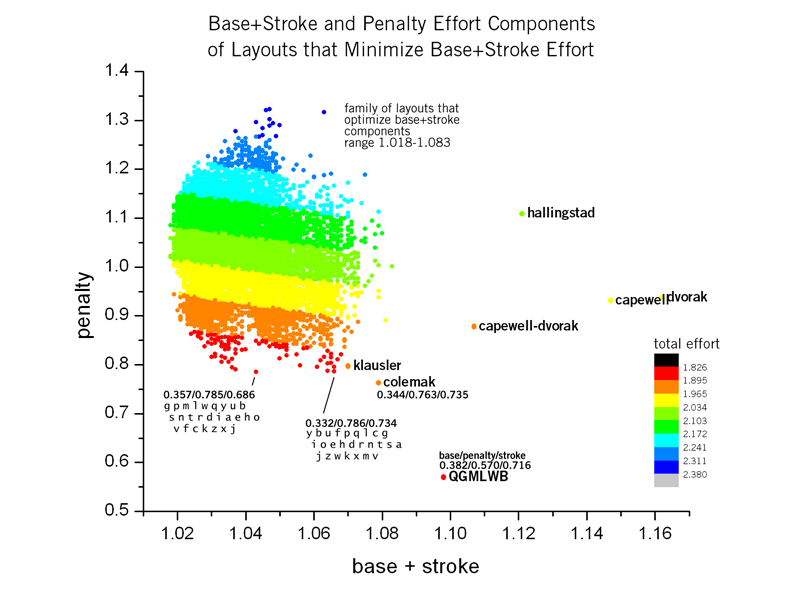
The solution set in the figure above was optimized using a 1:0:1 base:penalty:stroke ratio. With the exception of the penalty component, the solutions were competitive. Therefore, it is reasonable to suggest that by slightly increasing the penalty weight in this optimization, a layout could be found that has lower base effort and stroke than QGMLWB and a lower penalty than Colemak. The solutions to this kind of optimization, with a ratio of 10:1:10, are shown below.
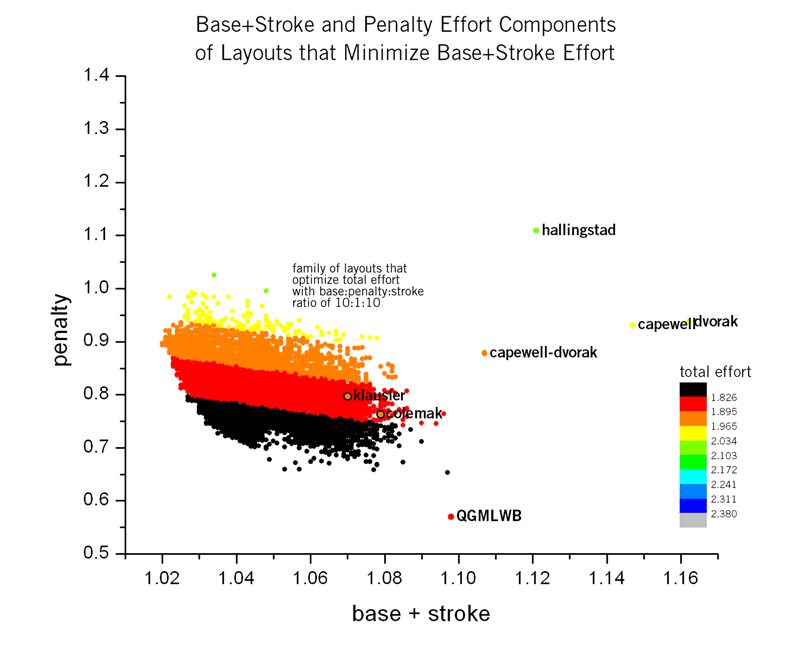
In Figure 12 many solutions have each of the three effort components lower than Colemak. Since it is not easy to see where these fall, I have plotted only these solutions in the figure below.
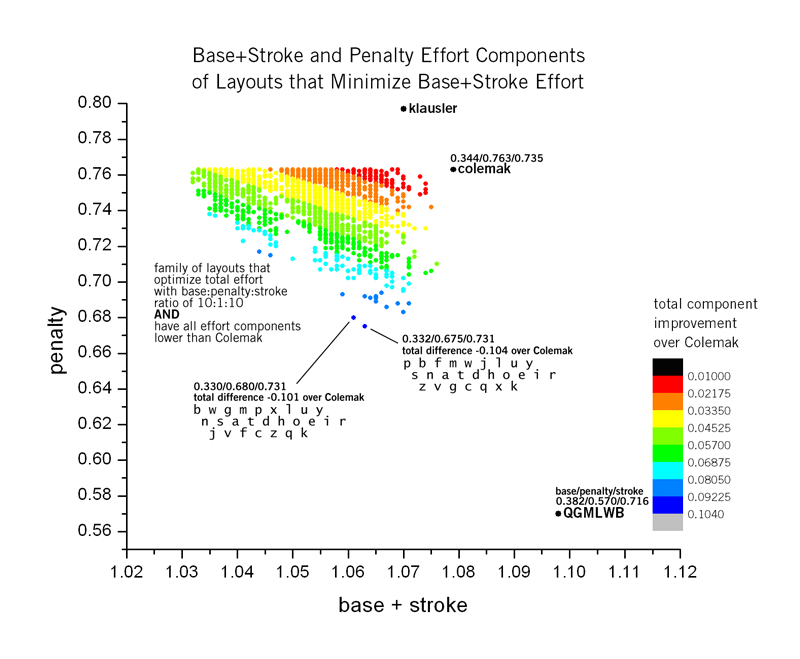
The layout with the largest total effort component improvement is the PBFMWJ, which has a better base effort (0.332 vs 0.344), penalty (0.675 vs 0.763) and stroke (0.731 vs 0.735) than Colemak. This layout improves over Colemak by 0.104. The next best improved layout is BWGMPX, with a -0.101 effort decrease.
| Colemak improvement | |||||
|---|---|---|---|---|---|
| model | keyboard | total effortrel% | effort contributionsrel% | ||
| base | penalties | path | |||
| mod_01 | colemak |
1.842
|
0.34418.7
|
0.76341.4
R0.158 F0.487 |
0.73539.9
|
| colemak-imp-01 |
1.738
(-5.6)
|
0.33219.1
(-3.5)
|
0.67538.8
(-11.5)
R0.148 (-6.3) F0.462 (-5.1) |
0.73142.1
(-0.5)
|
|
