The Ptolemaic Clock — A Proposal
contents
Consider the lowly wall clock. It's practical and generally tells the correct time. It's the same clock everywhere and after a while it gets boring pretty quickly—maybe now?
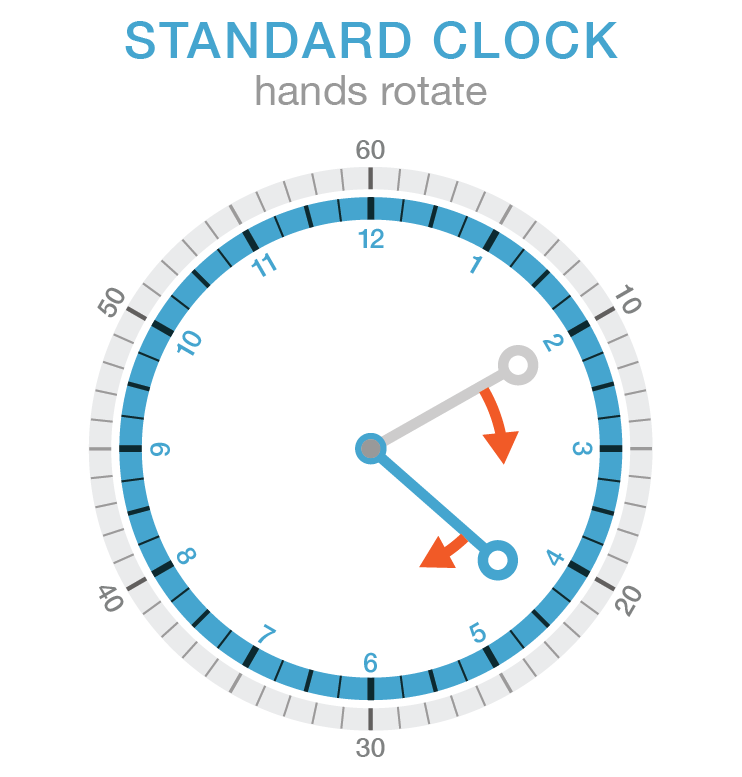
In the regular clock the face bezels stay in place and the hands move. Why am I telling you this? Well, maybe you see where I'm going.
Who says it's the hands that have to rotate? Instead of rotating hands and a stationary bezel, consider the clock with stationary hands rotating bezels.
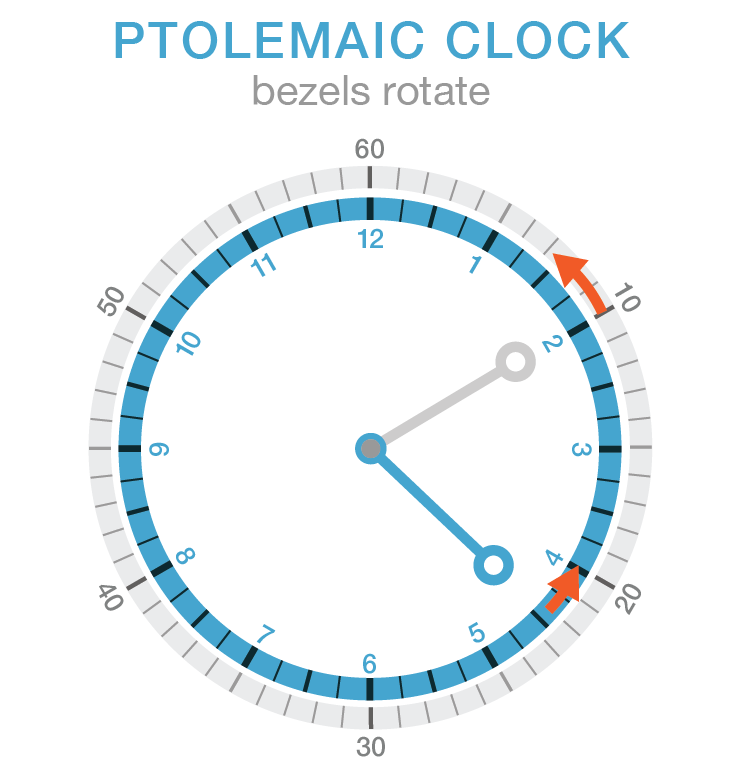
In the Ptolemaic clock there are two independent bezels and two independent hands. The bezels rotate counterclockwise to simulate the standard clockwise motion of the hands. The hands are not moving but in the frame of reference of the bezels, it's the hands that are rotating. The position of the bezel is always related to the current time and the position of its corresponding hand.
The bezel can move clockwise.
Thanks to Rodrigo Goya for suggesting the name for this kind of clock—Ptolemaic Clock, named so after the geocentric Ptolemaic model of the solar system.
To tell the time on the Ptolemaic clock is a process identical to using the standard clock. You look at the bezel numbers at the ends of the hour and minute hands.
On the fixed bezel layout, most people will take a short cut and tell the time by the position of the hands. This works as long as you have a standard clock. On a Ptolemaic clock the position of the hands tells you nothing.
Here is a Ptolemaic clock telling us it is 6:30. It uses the same position of hands as in the figures above.
You know this because the blue hour hand points to midway between 6 and 7 on the inner hour bezel and the grey minute hand points to 30 on the outer minute bezel.

After 15 minutes, it's 6:45 and our Ptolemaic clock bezels have moved a little bit.
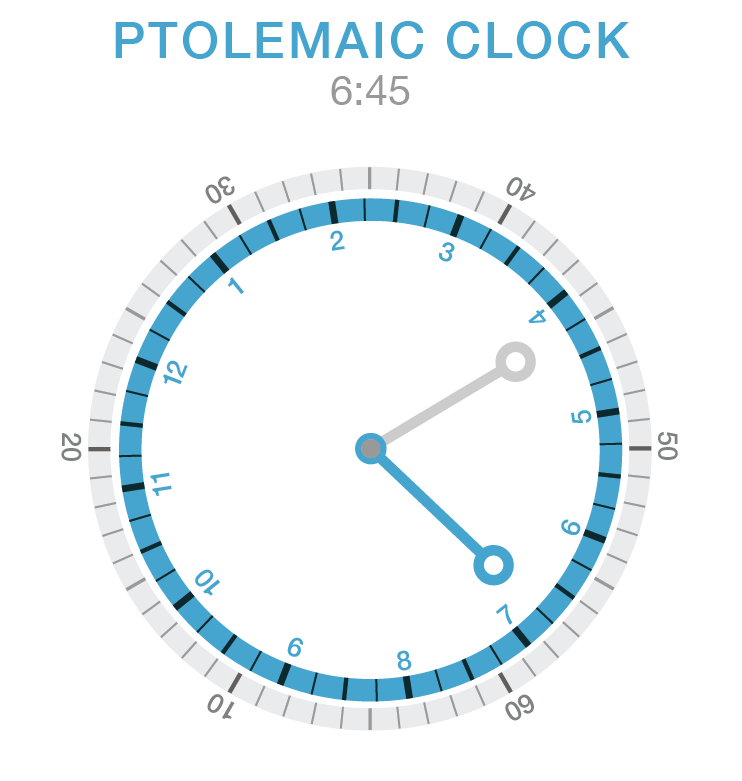
Can you tell what time it is on the Ptolemaic clock below?

Customizing your Ptolemaic clock is easy. Simply adjust the hands to desired positions and set the time by moving the bezels. The clock below shows the same time as the clock in the above figure — both show 8:50.
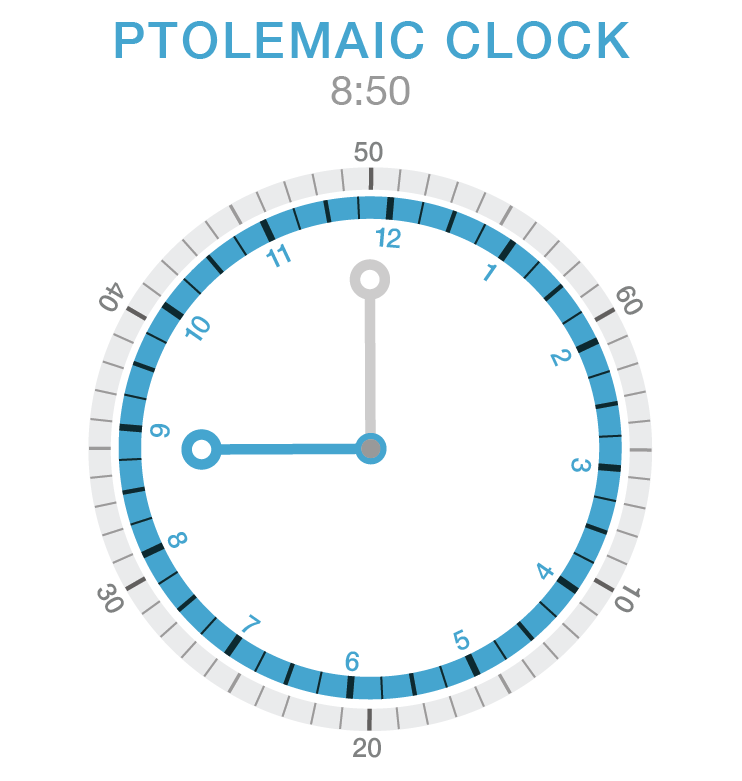
In the clock design shown here, the hands are the same size and only differ by color. To make things less confusing, emphasize the hour hand.
To make things more confusing, remove all color and number cues, keeping only a single symbol on each of the bezels to indicate 12 o'clock and 0 minutes. This is shown in the clock below.

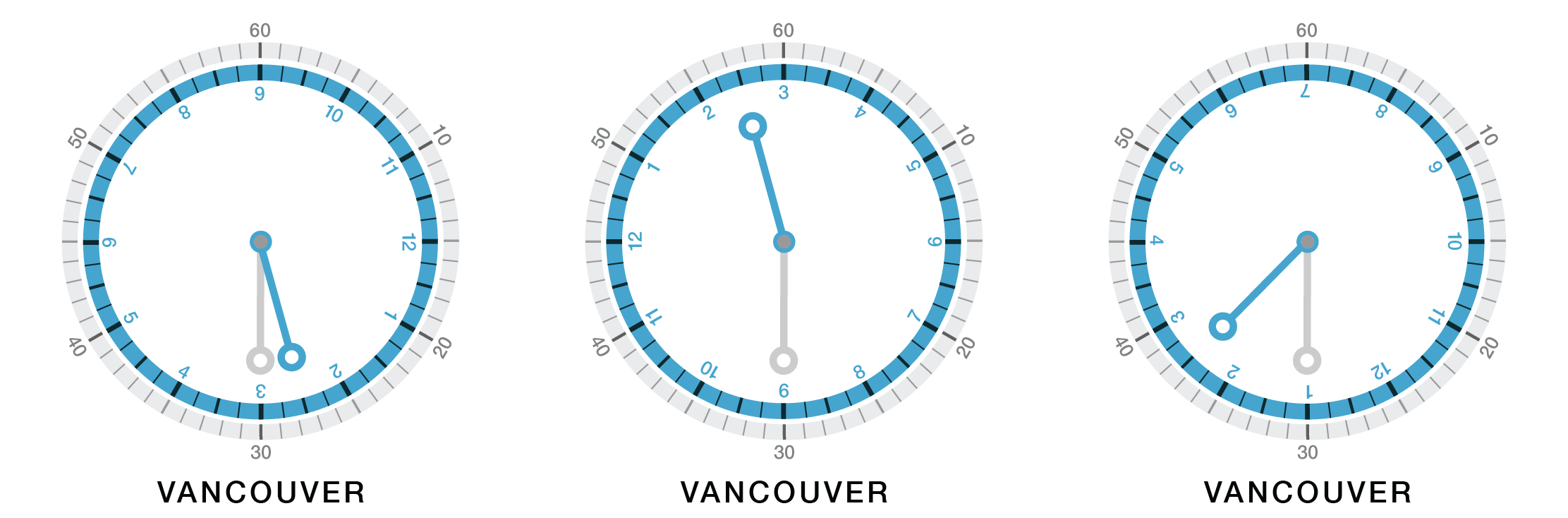
Spice it up with multiple Ptolemaic clocks side-by-side telling the same time with different hand positions.
Suppose it is 2:30 in Vancouver—this is my location. The clocks below all show 2:30, but with hands set to 5:30, 11:30 and 7:30.
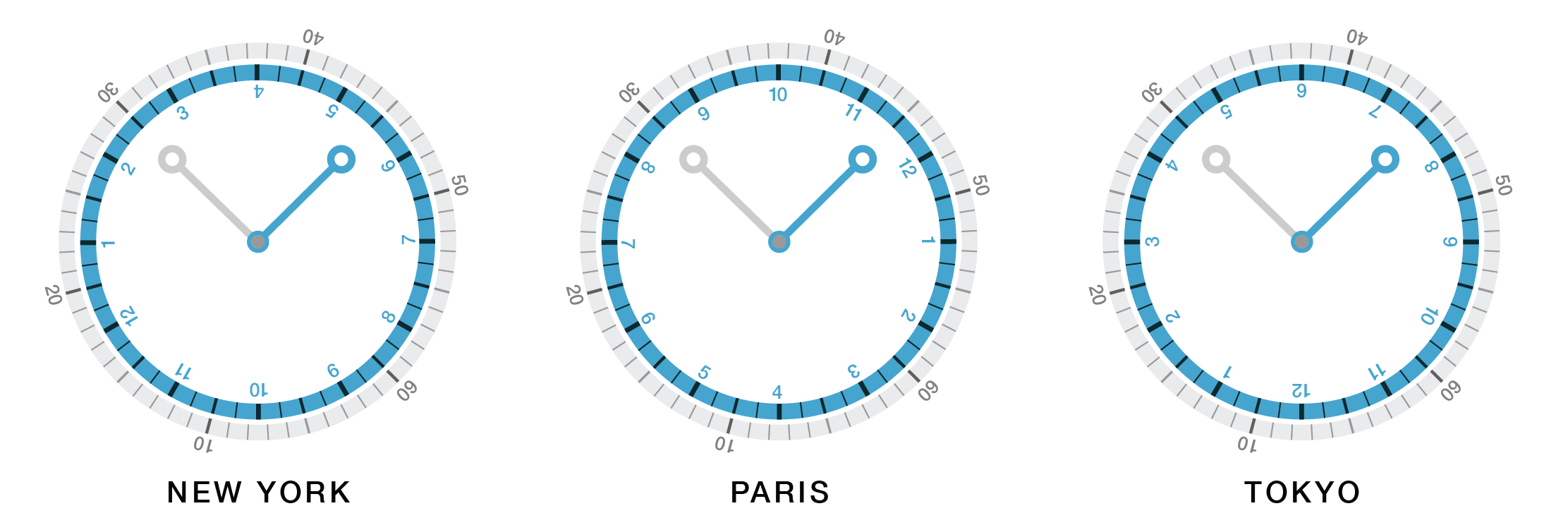
These hand positions are those that would appear on a standard clock showing the times in New York (5:30), Paris (11:30) and Tokyo (7:30).
Let's now use the Ptolemaic clock to show times at these three locations but with the hand set to the curiously satisfying layout of 10ish minutes to 2.
Set both hand positions to 12 o'clock and then remove the hands; to tell time, read the numbers on the hour and minute bezels at the apex of the clock.
Sophisticated implementations of the Ptolemaic clock could periodically randomize hand positions to keep things interesting; by the time you've figured out the time in the morning, you're wide awake.
Every minute the clock randomly resets its hand positions. The movement is smooth and the bezels follow.
If you would like to implement the Ptolemaic clock, I would be happy to hear from you. One should be able to take a regular wall clock, reverse the direction of the hand mechanism and rig a freely moving bezel to each of the minute and hour mechanism. The hands should not move and can be fixed to the front glass plate, for example.
It should now be clear that the Ptolemaic clock is superior to the standard clock. The reasons are
- it's much harder to tell time on the Ptolemaic clock, which makes your brain do more work
- it tips its hat off to a simpler time when we didn't know anything and hints at the possibility of regression anytime
- it will confuse everyone
- you have a great excuse for being late
- return to geocentric values!
- you can customize your own Ptolemaic clock by moving the hands to arbitrary locations
- two Ptolemaic clocks can have their hands and bezels at different positions but still be telling the same time
- two Ptolemaic clocks can have their hands at the same position but be telling different times
Nasa to send our human genome discs to the Moon
We'd like to say a ‘cosmic hello’: mathematics, culture, palaeontology, art and science, and ... human genomes.



Comparing classifier performance with baselines
All animals are equal, but some animals are more equal than others. —George Orwell
This month, we will illustrate the importance of establishing a baseline performance level.
Baselines are typically generated independently for each dataset using very simple models. Their role is to set the minimum level of acceptable performance and help with comparing relative improvements in performance of other models.
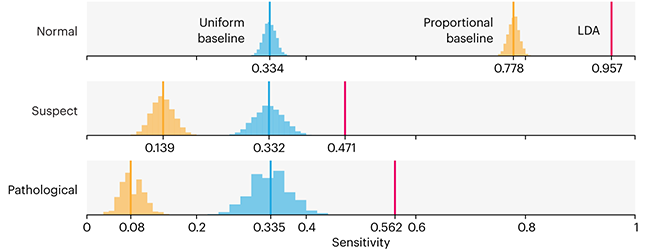
Unfortunately, baselines are often overlooked and, in the presence of a class imbalance5, must be established with care.
Megahed, F.M, Chen, Y-J., Jones-Farmer, A., Rigdon, S.E., Krzywinski, M. & Altman, N. (2024) Points of significance: Comparing classifier performance with baselines. Nat. Methods 20.
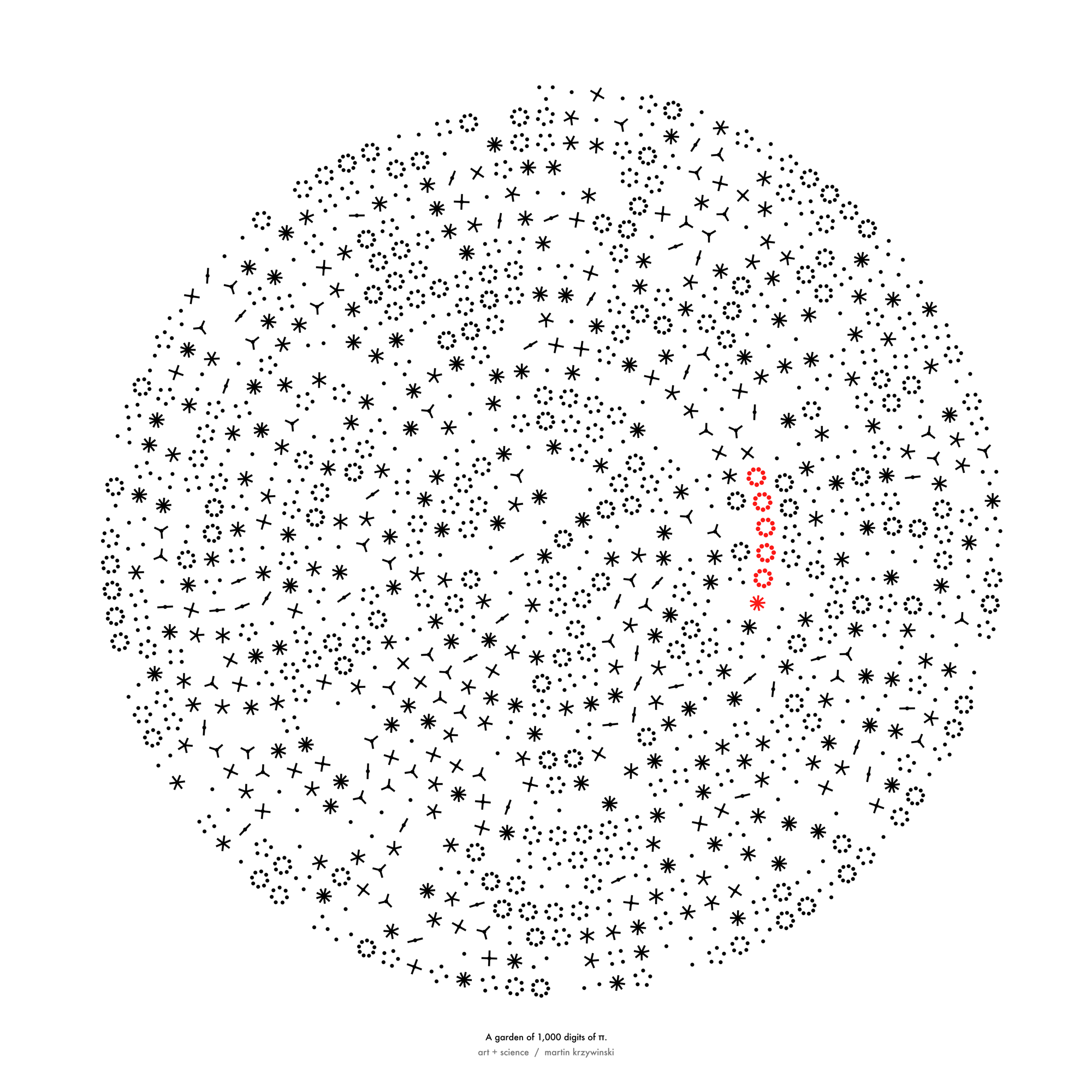
Happy 2024 π Day—
sunflowers ho!
Celebrate π Day (March 14th) and dig into the digit garden. Let's grow something.
How Analyzing Cosmic Nothing Might Explain Everything
Huge empty areas of the universe called voids could help solve the greatest mysteries in the cosmos.
My graphic accompanying How Analyzing Cosmic Nothing Might Explain Everything in the January 2024 issue of Scientific American depicts the entire Universe in a two-page spread — full of nothing.
The graphic uses the latest data from SDSS 12 and is an update to my Superclusters and Voids poster.
Michael Lemonick (editor) explains on the graphic:
“Regions of relatively empty space called cosmic voids are everywhere in the universe, and scientists believe studying their size, shape and spread across the cosmos could help them understand dark matter, dark energy and other big mysteries.
To use voids in this way, astronomers must map these regions in detail—a project that is just beginning.
Shown here are voids discovered by the Sloan Digital Sky Survey (SDSS), along with a selection of 16 previously named voids. Scientists expect voids to be evenly distributed throughout space—the lack of voids in some regions on the globe simply reflects SDSS’s sky coverage.”
voids
Sofia Contarini, Alice Pisani, Nico Hamaus, Federico Marulli Lauro Moscardini & Marco Baldi (2023) Cosmological Constraints from the BOSS DR12 Void Size Function Astrophysical Journal 953:46.
Nico Hamaus, Alice Pisani, Jin-Ah Choi, Guilhem Lavaux, Benjamin D. Wandelt & Jochen Weller (2020) Journal of Cosmology and Astroparticle Physics 2020:023.
Sloan Digital Sky Survey Data Release 12
Alan MacRobert (Sky & Telescope), Paulina Rowicka/Martin Krzywinski (revisions & Microscopium)
Hoffleit & Warren Jr. (1991) The Bright Star Catalog, 5th Revised Edition (Preliminary Version).
H0 = 67.4 km/(Mpc·s), Ωm = 0.315, Ωv = 0.685. Planck collaboration Planck 2018 results. VI. Cosmological parameters (2018).
constellation figures
stars
cosmology
Error in predictor variables
It is the mark of an educated mind to rest satisfied with the degree of precision that the nature of the subject admits and not to seek exactness where only an approximation is possible. —Aristotle
In regression, the predictors are (typically) assumed to have known values that are measured without error.
Practically, however, predictors are often measured with error. This has a profound (but predictable) effect on the estimates of relationships among variables – the so-called “error in variables” problem.
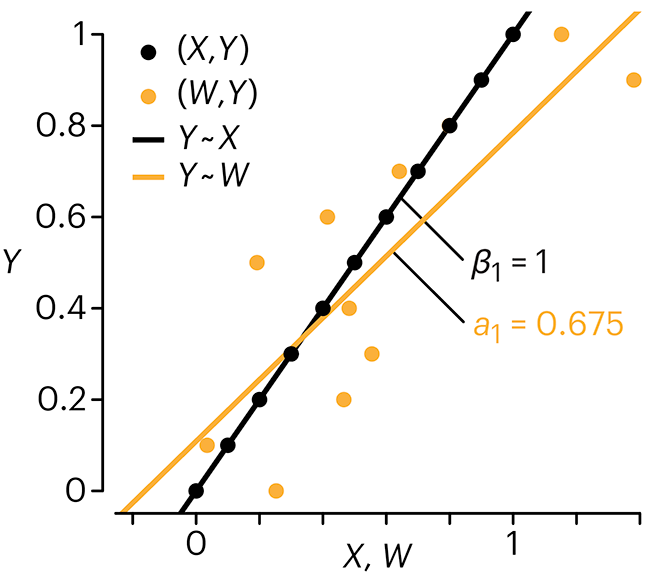
Error in measuring the predictors is often ignored. In this column, we discuss when ignoring this error is harmless and when it can lead to large bias that can leads us to miss important effects.
Altman, N. & Krzywinski, M. (2024) Points of significance: Error in predictor variables. Nat. Methods 20.
Background reading
Altman, N. & Krzywinski, M. (2015) Points of significance: Simple linear regression. Nat. Methods 12:999–1000.
Lever, J., Krzywinski, M. & Altman, N. (2016) Points of significance: Logistic regression. Nat. Methods 13:541–542 (2016).
Das, K., Krzywinski, M. & Altman, N. (2019) Points of significance: Quantile regression. Nat. Methods 16:451–452.
Convolutional neural networks
Nature uses only the longest threads to weave her patterns, so that each small piece of her fabric reveals the organization of the entire tapestry. – Richard Feynman
Following up on our Neural network primer column, this month we explore a different kind of network architecture: a convolutional network.
The convolutional network replaces the hidden layer of a fully connected network (FCN) with one or more filters (a kind of neuron that looks at the input within a narrow window).
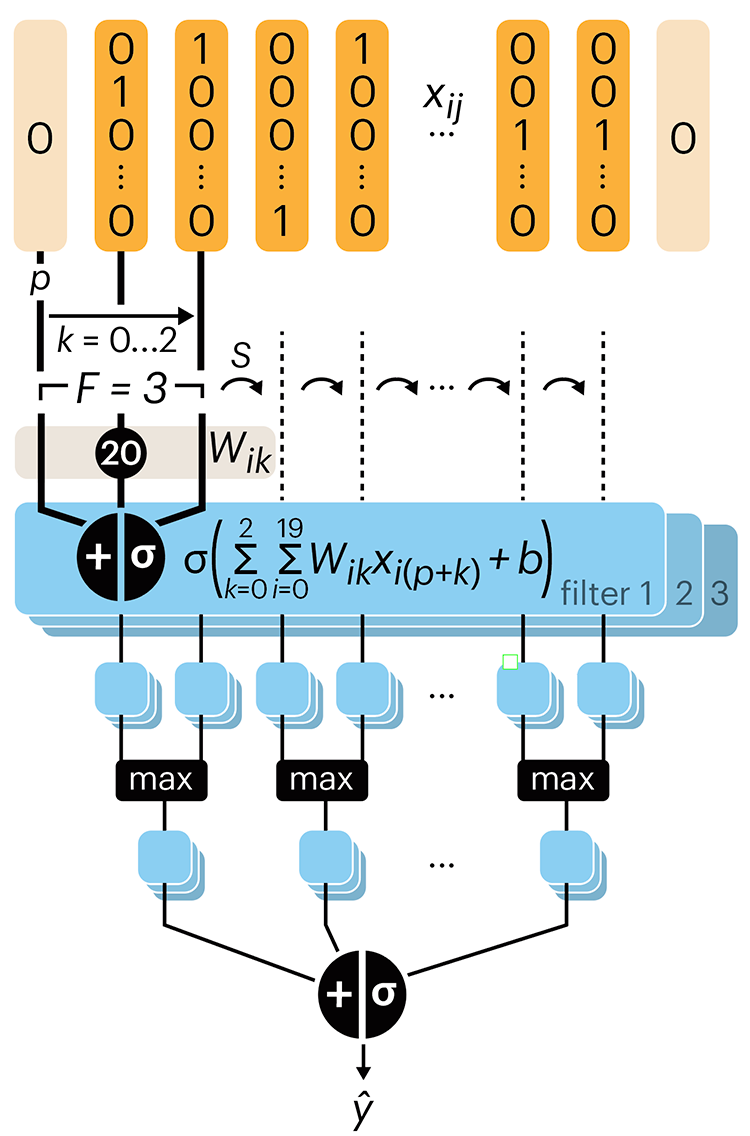
Even through convolutional networks have far fewer neurons that an FCN, they can perform substantially better for certain kinds of problems, such as sequence motif detection.
Derry, A., Krzywinski, M & Altman, N. (2023) Points of significance: Convolutional neural networks. Nature Methods 20:1269–1270.
Background reading
Derry, A., Krzywinski, M. & Altman, N. (2023) Points of significance: Neural network primer. Nature Methods 20:165–167.
Lever, J., Krzywinski, M. & Altman, N. (2016) Points of significance: Logistic regression. Nature Methods 13:541–542.