This service, like all my online color resources, is absolutely free to use with no restrictions or ads.
If you find it useful, your donation would be a way to say thanks.
the image color summarizer
The colour summarizer will produce descriptive colour statistics for an image. Reported will be the average, median, minimum and maximum of each component of RGB, HSV, LCH and Lab. Average hues are calculated using mean of circular quantities.
Some of the questions the summarizer will answer are
- what is the average color hue, saturation and value in my image?
- what are the colours that are most representative of the image?
- what is the image's human readable colour description (e.g. dark pure blue)?
- what do the RGB, HSV, LCH and Lab histograms look like?
- what are the RGB, HSV, LCH and Lab pixel values?
The color clustering function tells you the representative colors of the image and shows you how the pixels in the image partition into groups.
The method works well on images with relatively well-defined color boundaries and not well on images with smooth gradients that transition across a large range of colors (in hue, brightness and saturation).
If you want to find specific colors or snap colors to reference colors then clustering isn't for you. Instead, kuse my colorsnap application.
PERCEPTUAL IMAGE DATA WITH LCH
LCH is the perceptually uniform equivalent of HSV, and defines colors using intuitive and perceptually-based luminance (perceived brightness), chroma (richness) and hue. If you are doing any kind of image analysis, it's likely that LCH will be much more useful to you than HSV or RGB.
To learn about LCH, see my presentation about color spaces and perceptual uniformity.
USE THE API
If you are a data geek, you'll be happy to know that XML or plain-text API output of the image statistics now includes RGB and HSV histograms, as well as individual pixel values. Munge away!
The purpose of this utility is to generate metadata that summarizes an image's colour characteristics for inclusion in an image database, such as Flickr. In particular this tool is being used to generate metadata for Flickr's Color Fields group.
get started already
If you are curious, see the summarizer run or look at examples. Of course, why not provide your own image for analysis? You should read the FAQ to see how things work.
color summarizer web service
I also provide a simple web service. See a plain-text output or XML output of this analysis.
an example
A little car—lonely, broken and in Havana. I know that feeling.
Here's how the color summarizer describes this image:
altitude antidote aqua beau black blue botticelli bronze brown cod columbia cork dark derby desert drought dust eighth escape geebung goldenrod grey half joss judge jungle kabul malta mash medium metallic millbrook mist moleskin nullarbor pale paperback parchment pizza rich rickshaw road rock rocky rodeo smoky soho sweetwaters triple yellow ziggurat
a counter example
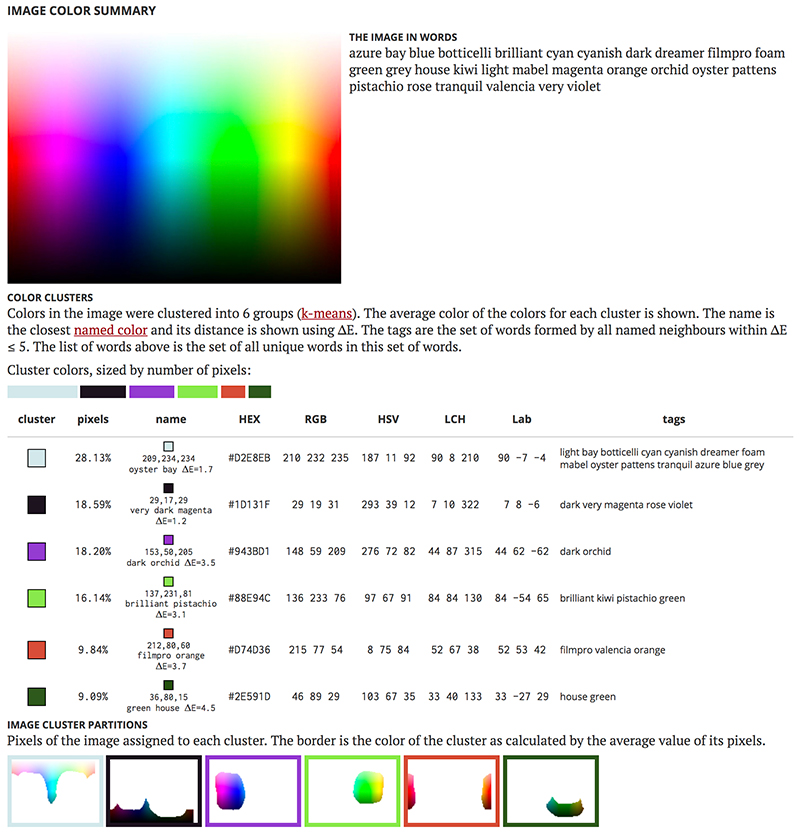
If you feed in an image with all the colors, you'll get out at worst garbage and at best arbitrary and irreproducible clusters. Below is a Granger rainbow grouped into 6 clusters.
By asking for 6 clusters we got: (1) everything that's bright and desaturated, (2) everthing that's dark, (3) purple/blues, (4) bright saturated green/yellows, (5) reds and (6) saturated dark greens.
issues
Image statistics are computed using every pixel in the image. Therefore, analysis of images in which the background is dominant will be skewed by the background color. Specifically, statistics for product images (e.g. an items photographed on a white background) can be difficult to interpret.
The answer to this is to mask areas (e.g. white, or close to white) of the image before carrying out statistics, but this is not implemented. But it will be soon.