`\pi` Day 2018 Art Posters - Stitched city road maps from around the world
On March 14th celebrate `\pi` Day. Hug `\pi`—find a way to do it.
For those who favour `\tau=2\pi` will have to postpone celebrations until July 26th. That's what you get for thinking that `\pi` is wrong. I sympathize with this position and have `\tau` day art too!
If you're not into details, you may opt to party on July 22nd, which is `\pi` approximation day (`\pi` ≈ 22/7). It's 20% more accurate that the official `\pi` day!
Finally, if you believe that `\pi = 3`, you should read why `\pi` is not equal to 3.
And if you've got to sleep a moment on the road
I will steer for you
And if you want to work the street alone
I'll disappear for you
—Leonard Cohen (I'm Your Man)
This year's is the 30th anniversary of `\pi` day. The theme of the art is bridging the world and making friends. So myself I again team up with my long-time friend and collaborator Jake Lever. I worled with Jake on the snowflake catalogue, where we build a world of flakes.
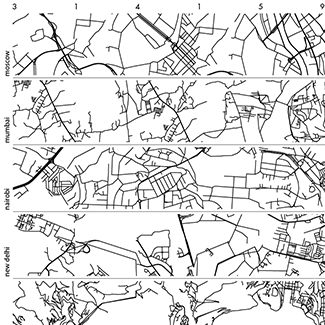
And so, this year we also build a world. We start with all the roads in the world and stitch them together in brand new ways. And if you walk more than 1 km in this world, you'll likely to be transported somewhere completely different.
This year's `\pi` day song is Trance Groove: Paris. Why? Because it's worth to go to new places—real or imagined.
The input data set to the art are all the roads in the world, as obtained from Open Street Map.
Road segments between intersections are represented by polylines and ends at intersections are snapped together to coincide with a resolution of 5–10 meters.
There are 108,366,429 polylines and together they span about 39,930,000 km.
extracting cities
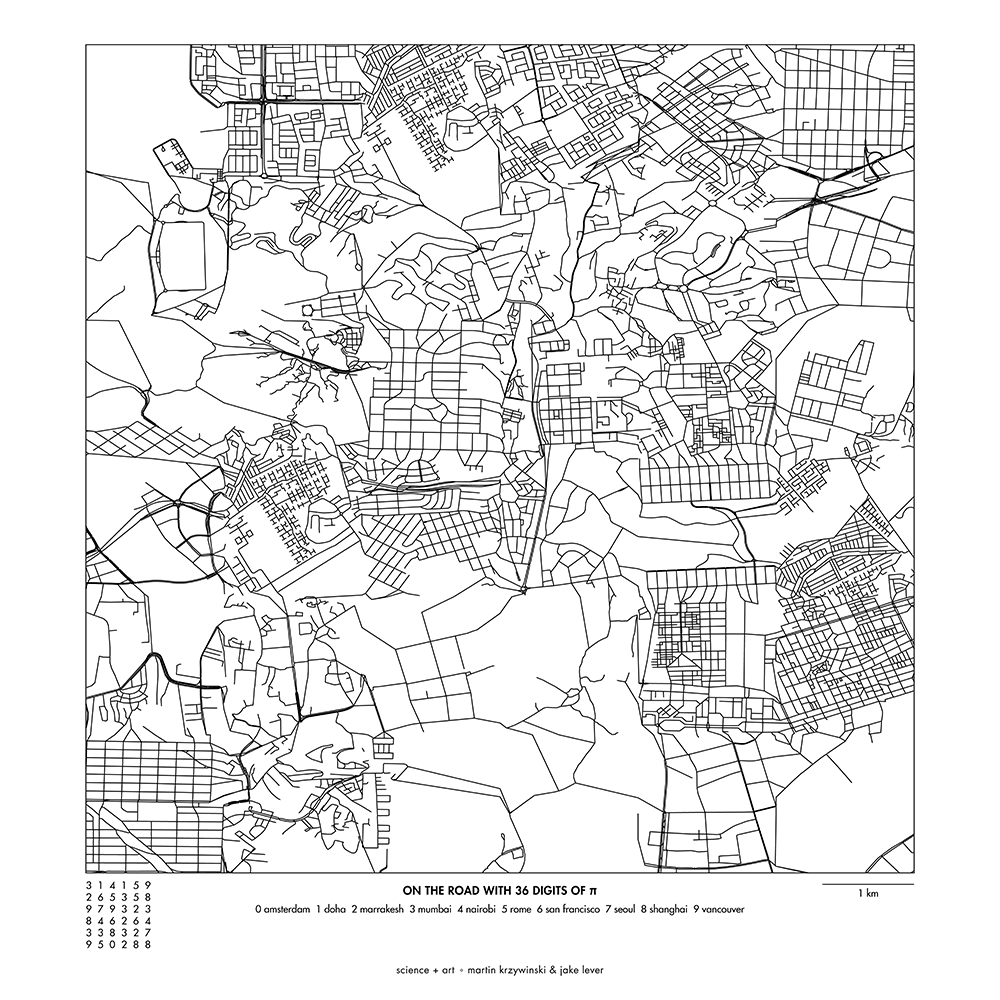
We took 44 cities and sampled a square patch of 0.6 × 0.6 degrees of roads from the data set centered on the longitude and latitude coordinates below. This roughly corresponds to a square of 65 km × 65 km.
These center coordinates might be slightly different from the canonical ones associated with a city—I used Google Maps to center the coordinates on what I felt was a useful center for sampling streets. Below are these coordinates along with the number of polylines extracted.
CITY LATITUDE LONGITUDE POLYLINES
--------------- ------------ ------------- ---------
amsterdam 52.38179720 4.90840330 98,965
bangkok 13.72635950 100.53609560 154,348
barcelona 41.38759720 2.17333560 86,575
beijing 39.90487690 116.39331750 49,867
berlin 52.51864170 13.40732310 64,336
buenos_aires -34.61566250 -58.50333750 267,432
cairo 30.05371250 31.23528970 108,524
copenhagen 55.67346250 12.58781160 45,025
doha 25.28233490 51.53479620 50,458
dublin 53.34316360 -6.24433520 44,109
edinburgh 55.94884870 -3.18828100 34,211
hong_kong 22.31338230 114.16994610 36,329
istanbul 41.03592820 28.98158110 190,938
jakarta -6.21858830 106.85252890 253,211
johannesburg -26.20653880 28.05113830 128,840
lisbon 38.73064000 -9.13667460 98,118
london 51.50838960 -0.08585320 169,164
los_angeles 34.04362360 -118.24505510 193,899
madrid 40.41671290 -3.70329570 112,495
marrakesh 31.63192610 -7.98895890 17,442
melbourne -37.88286720 145.11800540 140,817
mexico_city 19.39741470 -99.15827060 273,477
moscow 55.75202630 37.61531070 40,043
mumbai 19.18775070 72.97777590 65,316
nairobi -1.28718700 36.83157870 31,317
new_delhi 28.61245350 77.21369970 262,503
new_york 40.72187290 -73.92426750 199,652
nice 43.70006260 7.26974590 25,564
osaka 34.66944300 135.49965600 376,652
paris 48.85837360 2.29229260 175,028
prague 50.08022370 14.43002100 58,659
rome 41.89659480 12.49983650 81,370
san_francisco 37.77526950 -122.40966350 82,462
sao_paulo -23.57343700 -46.63341590 267,742
seoul 37.54869140 126.99479350 169,593
shanghai 31.22590500 121.47386710 50,036
st_petersburg 59.93029690 30.33955910 31,186
stockholm 59.32318770 18.07408060 48,321
sydney -33.86772020 151.20734660 76,820
tokyo 35.69220740 139.75613010 694,893
toronto 43.66328030 -79.38932030 73,173
vancouver 49.25782630 -123.19394300 34,081
vienna 48.20740250 16.37336040 53,669
warsaw 52.23101840 21.01639680 54,870
Each city's road coordinates were then transformed using the equirectangular projection to make the distance between longitude meridians constant with latitude. This was done by $$ \phi' \leftarrow \phi - \text{avg}(\phi) $$ $$ \lambda' \leftarrow (\lambda - avg(\lambda)) \text{cos} (avg(\phi)) $$
where `\phi` is the latitude and `\lambda` is the longitude. The average is taken over the patch of roads extracted for the city. For all steps below these transformed coordinates were used.
copenhagen
Let's look at one city—Copenhagen—to get a feel for the data set.
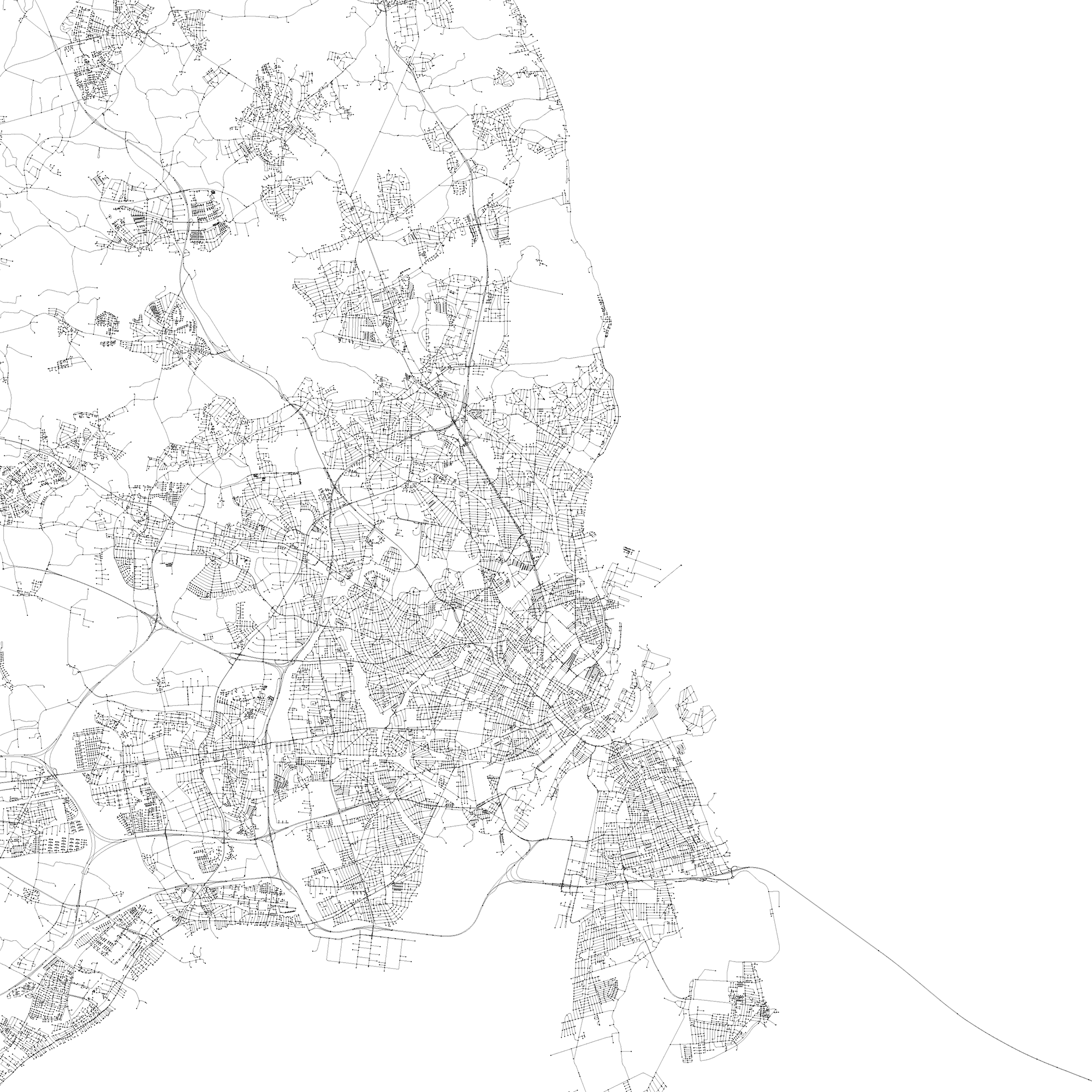
In the zoom crop below, you can see the intersections (dots) and the individual polylines that connect the intersections.
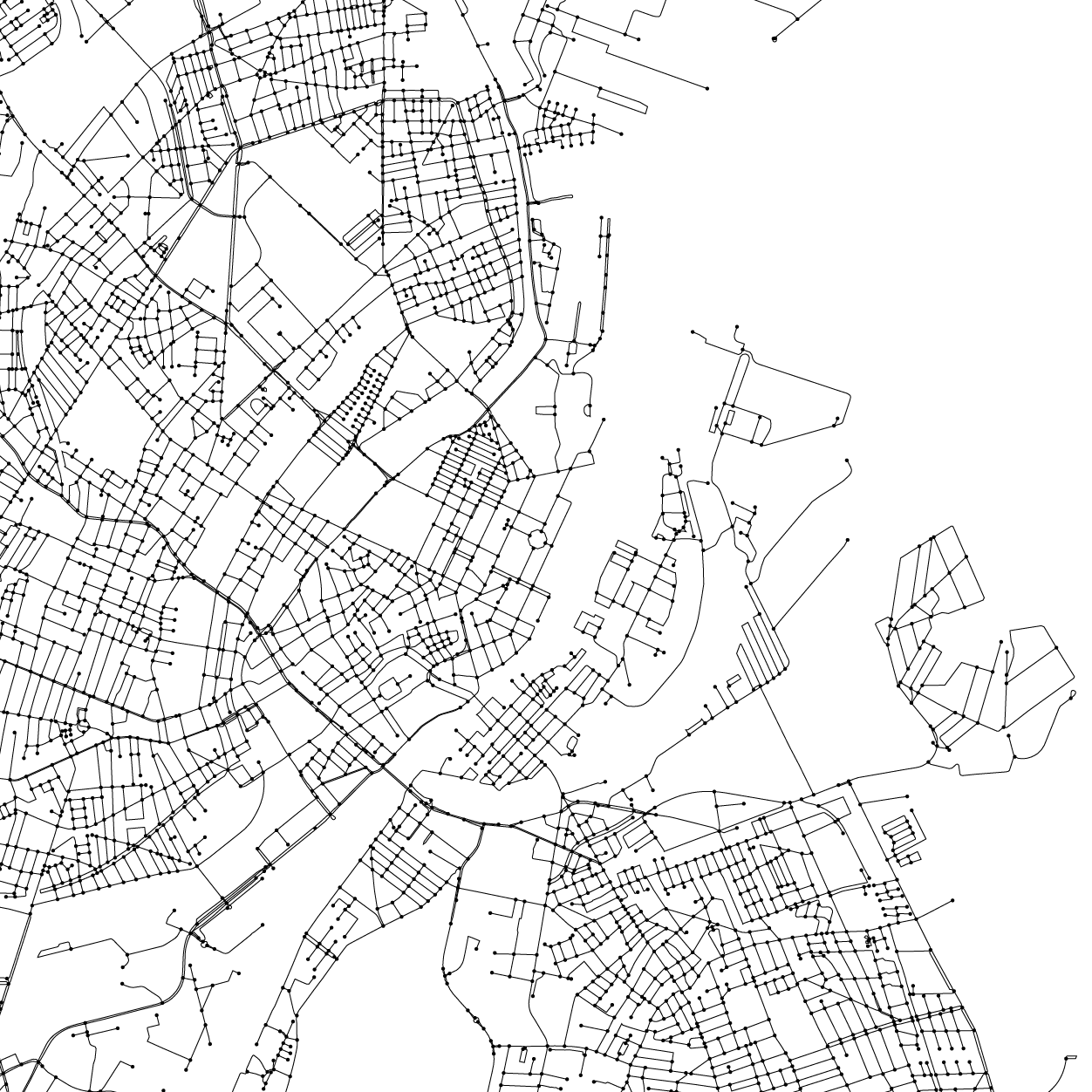
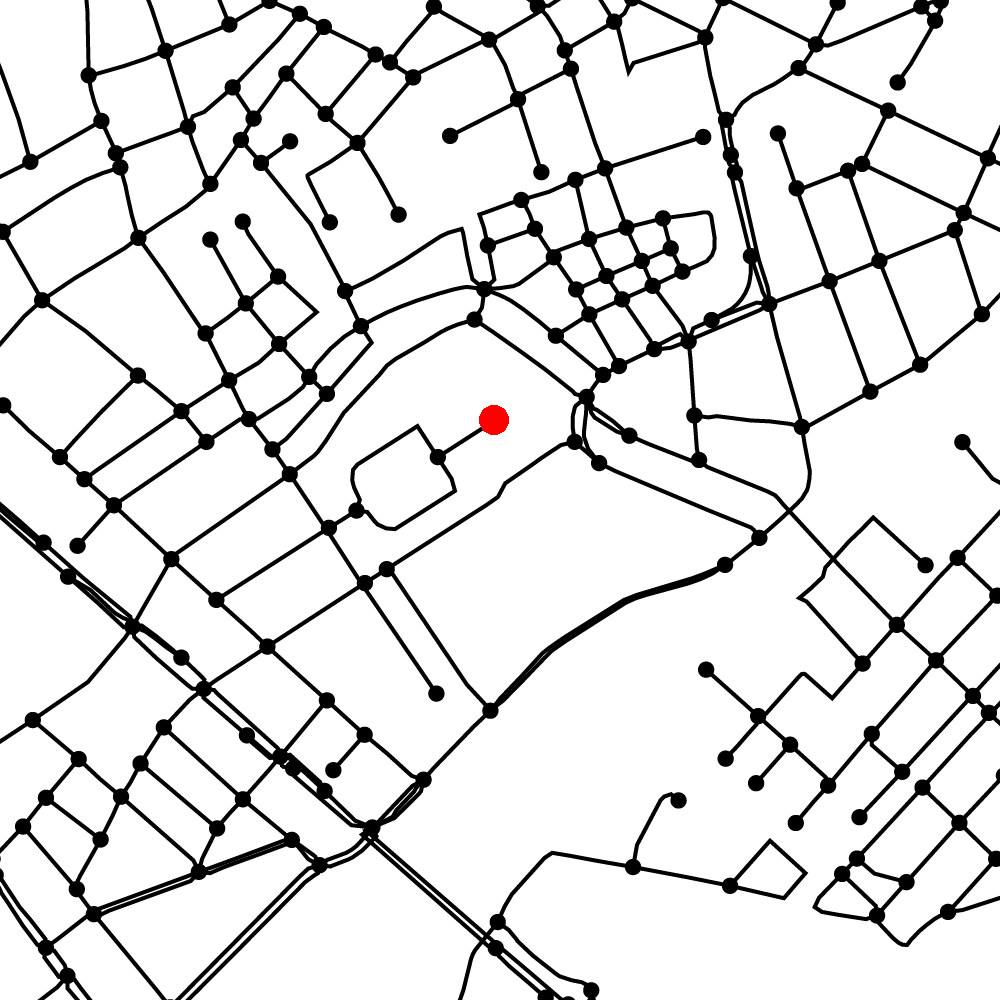
Zooming in even more you can see the Christiansborg Slot, one of the Danish Palaces and the seat of the Danish Parliament (corresponding Google Map view).
creating city strips
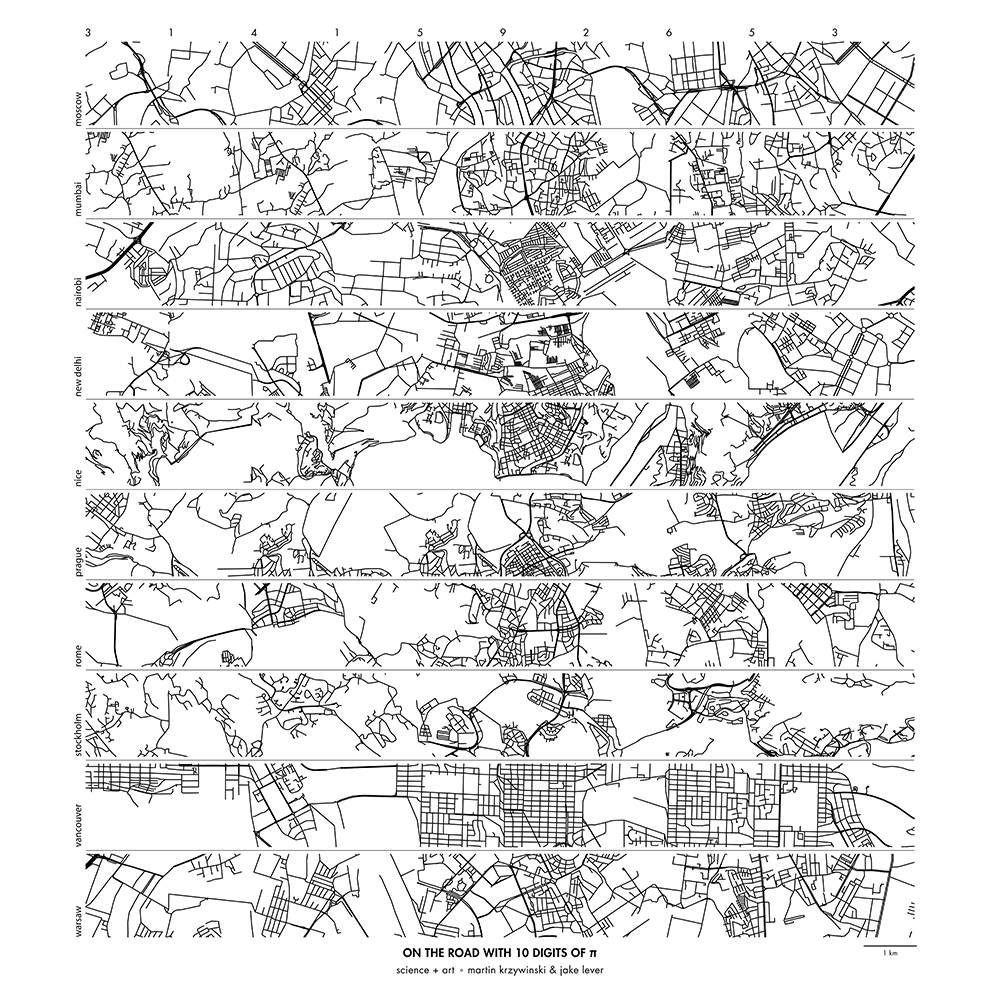
City strips were created by sampling patches of 0.015 × 0.015 degrees (after transformation). This corresponds roughly to 1.7 km.
For each position in the strip, patches were sampled in order of the digits of `\pi` only if the number of polylines in the was `40d \le N < 40(d+1)-1` where `d` is the digit of `\pi`. Patches for `d=9` only need to have `360 \le N` polylines.
For example, the first patch is assigned to `d=3` and it must have `120 \le N < 159` polylines. The second patch is sampled so that its density is `40 \le N < 79` because it is associated with the next digit, `d=1`.
Further selection on acceptable patches is performed so that the streets line up with the previous patch. Minor local adjustments and stitching are performed to make the join appear seamless.
Below is an example of a set of city strips for Amsterdam, Bangkok, Beijing, Berlin, Copenhagen, Edinburgh, Hong Kong, Johannesburg, Marrakesh and Melbourne.
 buy artwork
buy artwork
Below I zoom in on a portion of the city strips above to show the result of the stitching—individual street patches are outlined in blue squares.
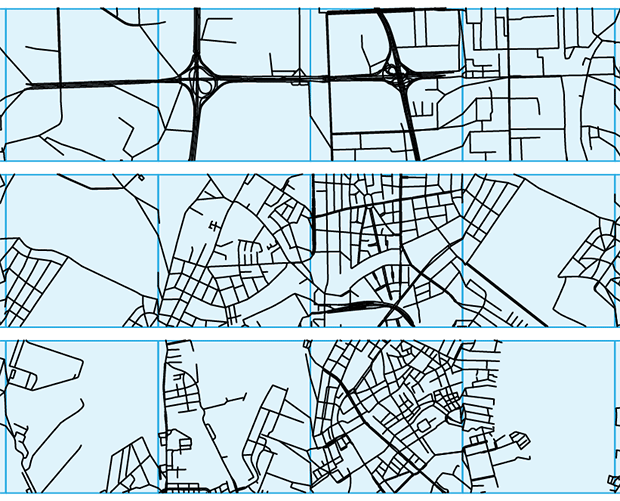
It's interesting to see that some patches (e.g. 4th one on the bottom strip, which is Copenhagen) don't necessarily have roads that across the patch horizontally.
creating world patches
World patches are a two-dimension version of city strips but they use more than one city.
Patches are sampled from cities based on the order of the digits of `\pi`, as arranged on a 6 × 6 grid. For example, the first row of patches corresponds to 314159 and the second 265358. Each digit is assigned to a city from which the corresponding patch is sampled.
As for city strips, patches are selected only if they align with previous patches. This is now trickier to do in two-dimensions because we must match a selected patch with up to two other patches already placed.
Unlike for city strips, there is no selection made for street density.
Below is a world patch using the following digit-to-city assignment: 0:Amsterdam, 1:Doha, 2:Marrakesh, 3:Mumbai, 4:Nairobi, 5:Rome, 6:San Francisco, 7:Seoul, 8:Shanghai and 9:Vancouver.
 buy artwork
buy artwork
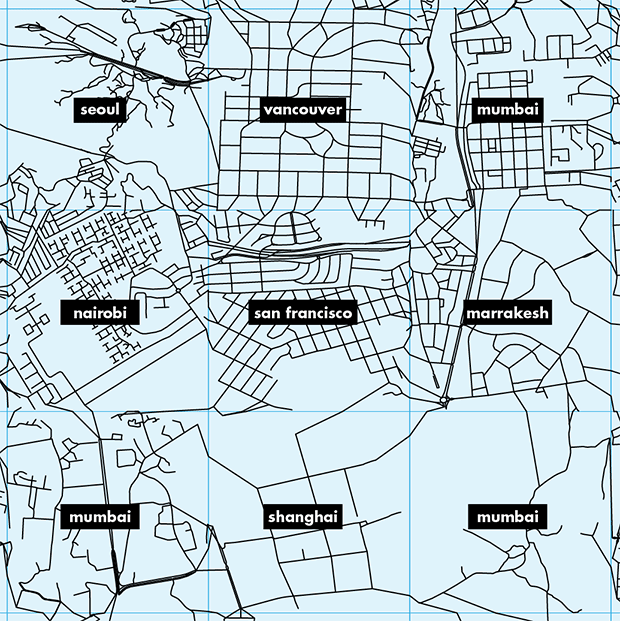
Below I zoom in on patches in the center of the image and show the cities from which the patches were sampled.
Nasa to send our human genome discs to the Moon
We'd like to say a ‘cosmic hello’: mathematics, culture, palaeontology, art and science, and ... human genomes.



Comparing classifier performance with baselines
All animals are equal, but some animals are more equal than others. —George Orwell
This month, we will illustrate the importance of establishing a baseline performance level.
Baselines are typically generated independently for each dataset using very simple models. Their role is to set the minimum level of acceptable performance and help with comparing relative improvements in performance of other models.
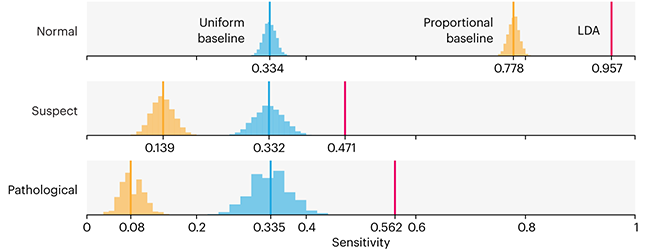
Unfortunately, baselines are often overlooked and, in the presence of a class imbalance5, must be established with care.
Megahed, F.M, Chen, Y-J., Jones-Farmer, A., Rigdon, S.E., Krzywinski, M. & Altman, N. (2024) Points of significance: Comparing classifier performance with baselines. Nat. Methods 20.
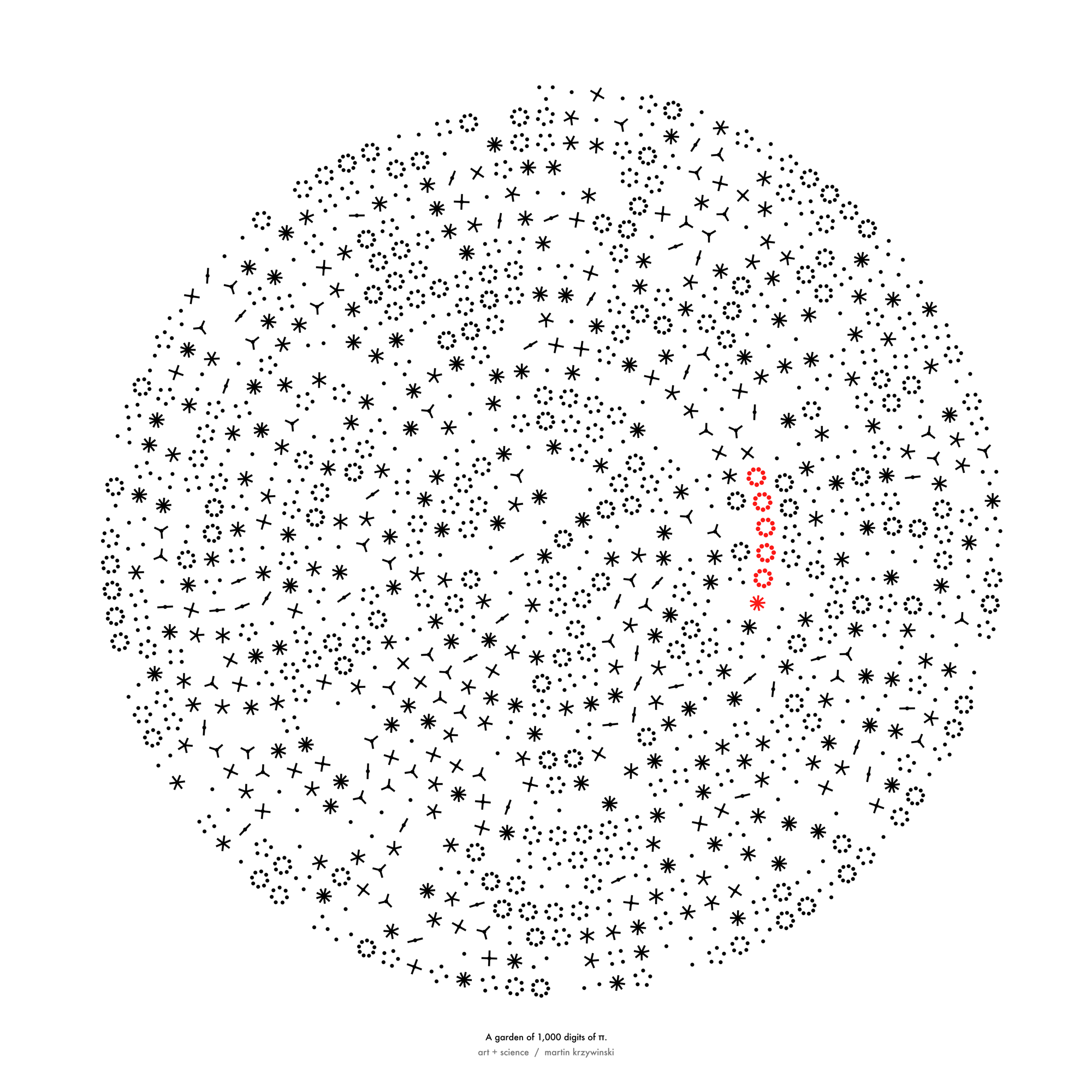
Happy 2024 π Day—
sunflowers ho!
Celebrate π Day (March 14th) and dig into the digit garden. Let's grow something.
How Analyzing Cosmic Nothing Might Explain Everything
Huge empty areas of the universe called voids could help solve the greatest mysteries in the cosmos.
My graphic accompanying How Analyzing Cosmic Nothing Might Explain Everything in the January 2024 issue of Scientific American depicts the entire Universe in a two-page spread — full of nothing.
The graphic uses the latest data from SDSS 12 and is an update to my Superclusters and Voids poster.
Michael Lemonick (editor) explains on the graphic:
“Regions of relatively empty space called cosmic voids are everywhere in the universe, and scientists believe studying their size, shape and spread across the cosmos could help them understand dark matter, dark energy and other big mysteries.
To use voids in this way, astronomers must map these regions in detail—a project that is just beginning.
Shown here are voids discovered by the Sloan Digital Sky Survey (SDSS), along with a selection of 16 previously named voids. Scientists expect voids to be evenly distributed throughout space—the lack of voids in some regions on the globe simply reflects SDSS’s sky coverage.”
voids
Sofia Contarini, Alice Pisani, Nico Hamaus, Federico Marulli Lauro Moscardini & Marco Baldi (2023) Cosmological Constraints from the BOSS DR12 Void Size Function Astrophysical Journal 953:46.
Nico Hamaus, Alice Pisani, Jin-Ah Choi, Guilhem Lavaux, Benjamin D. Wandelt & Jochen Weller (2020) Journal of Cosmology and Astroparticle Physics 2020:023.
Sloan Digital Sky Survey Data Release 12
Alan MacRobert (Sky & Telescope), Paulina Rowicka/Martin Krzywinski (revisions & Microscopium)
Hoffleit & Warren Jr. (1991) The Bright Star Catalog, 5th Revised Edition (Preliminary Version).
H0 = 67.4 km/(Mpc·s), Ωm = 0.315, Ωv = 0.685. Planck collaboration Planck 2018 results. VI. Cosmological parameters (2018).
constellation figures
stars
cosmology
Error in predictor variables
It is the mark of an educated mind to rest satisfied with the degree of precision that the nature of the subject admits and not to seek exactness where only an approximation is possible. —Aristotle
In regression, the predictors are (typically) assumed to have known values that are measured without error.
Practically, however, predictors are often measured with error. This has a profound (but predictable) effect on the estimates of relationships among variables – the so-called “error in variables” problem.
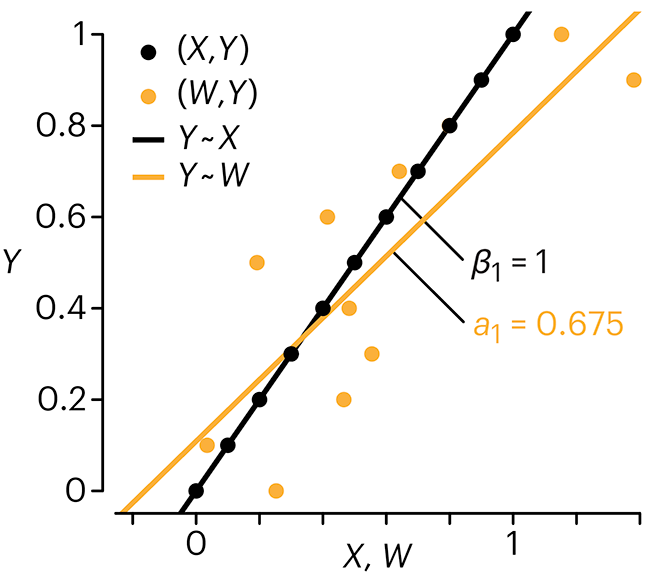
Error in measuring the predictors is often ignored. In this column, we discuss when ignoring this error is harmless and when it can lead to large bias that can leads us to miss important effects.
Altman, N. & Krzywinski, M. (2024) Points of significance: Error in predictor variables. Nat. Methods 20.
Background reading
Altman, N. & Krzywinski, M. (2015) Points of significance: Simple linear regression. Nat. Methods 12:999–1000.
Lever, J., Krzywinski, M. & Altman, N. (2016) Points of significance: Logistic regression. Nat. Methods 13:541–542 (2016).
Das, K., Krzywinski, M. & Altman, N. (2019) Points of significance: Quantile regression. Nat. Methods 16:451–452.
Convolutional neural networks
Nature uses only the longest threads to weave her patterns, so that each small piece of her fabric reveals the organization of the entire tapestry. – Richard Feynman
Following up on our Neural network primer column, this month we explore a different kind of network architecture: a convolutional network.
The convolutional network replaces the hidden layer of a fully connected network (FCN) with one or more filters (a kind of neuron that looks at the input within a narrow window).
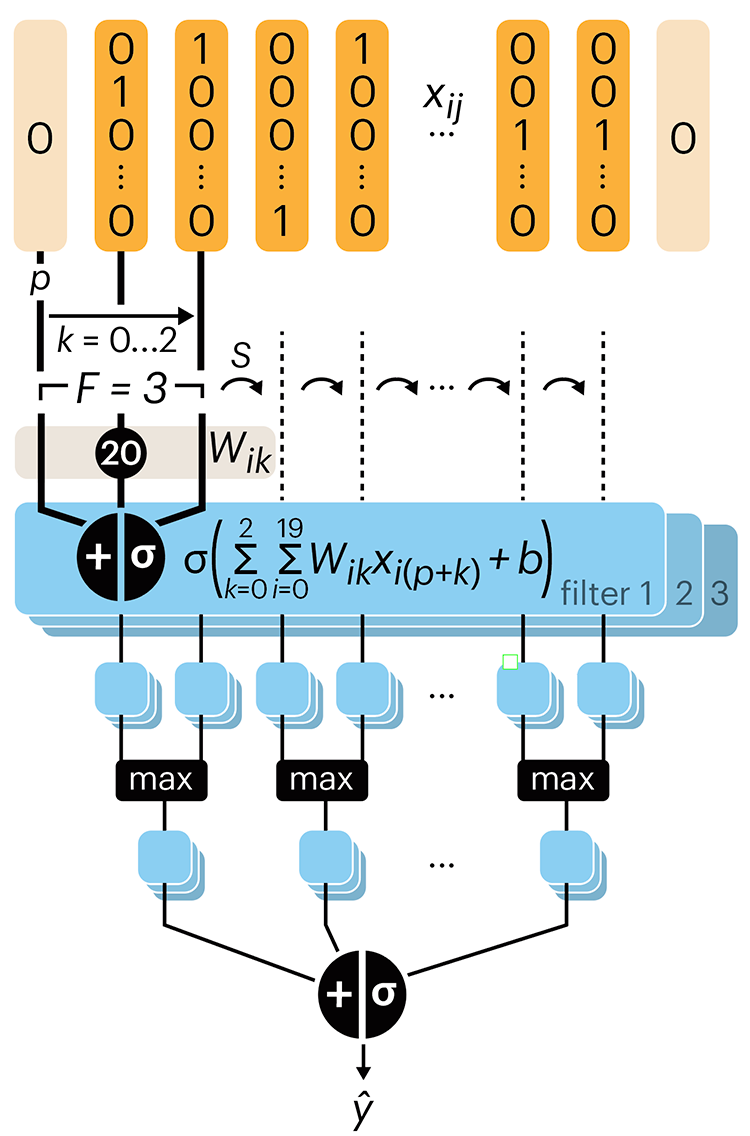
Even through convolutional networks have far fewer neurons that an FCN, they can perform substantially better for certain kinds of problems, such as sequence motif detection.
Derry, A., Krzywinski, M & Altman, N. (2023) Points of significance: Convolutional neural networks. Nature Methods 20:1269–1270.
Background reading
Derry, A., Krzywinski, M. & Altman, N. (2023) Points of significance: Neural network primer. Nature Methods 20:165–167.
Lever, J., Krzywinski, M. & Altman, N. (2016) Points of significance: Logistic regression. Nature Methods 13:541–542.