`\pi` Day 2014 Art Posters
On March 14th celebrate `\pi` Day. Hug `\pi`—find a way to do it.
For those who favour `\tau=2\pi` will have to postpone celebrations until July 26th. That's what you get for thinking that `\pi` is wrong. I sympathize with this position and have `\tau` day art too!
If you're not into details, you may opt to party on July 22nd, which is `\pi` approximation day (`\pi` ≈ 22/7). It's 20% more accurate that the official `\pi` day!
Finally, if you believe that `\pi = 3`, you should read why `\pi` is not equal to 3.
For the 2014 `\pi` day, two styles of posters are available: folded paths and frequency circles.
The folded paths show `\pi` on a path that maximizes adjacent prime digits and were created using a protein-folding algorithm.
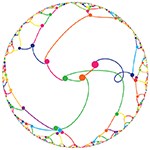
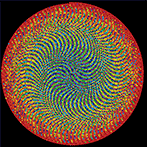
The frequency circles colourfully depict the ratio of digits in groupings of 3 or 6. Oh, look, there's the Feynman Point!
the many paths of `pi`—how to fold numbers

This year's Pi Day art expands on the work from last year, which showed Pi as colored circles on a grid. For those of you who really liked this minimalist depiction of π , I've created something slightly more complicated, but still stylish: Pi digit frequency circles. These are pretty and easy to understand. If you like random distribution of colors (and circles), these are your thing.
But to take drawing Pi a step further, I've experimented with folding its digits into a path. The method used is the same kind used to simulate protein folding. Research into protein folding is very active — the 3-dimensional structure of proteins is necessary for their function. Understanding how structure is affected by changes to underlying sequence is necessary for identifying how things go wrong in a cell.

method — folding a number
I will be using the replica exchange Monte Carlo algorithm to create folded paths (download code).
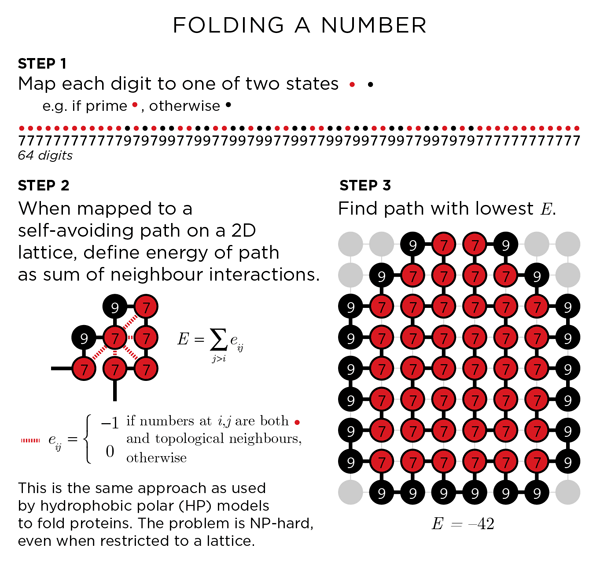
The choice of mapping between digit (0-9) and state (polar, hydrophobic) is arbitrary. I have chosen to assign the prime digits (2, 3, 5, 7) as hydrophobic. Another way can be to use perfect squares (1, 2, 4, 9). I construct the path by assigning each digit to a path node. One can partition π into two (or more) digit groupings (31, 41, 59, 26, ...) as well.
folding 64 digits of π
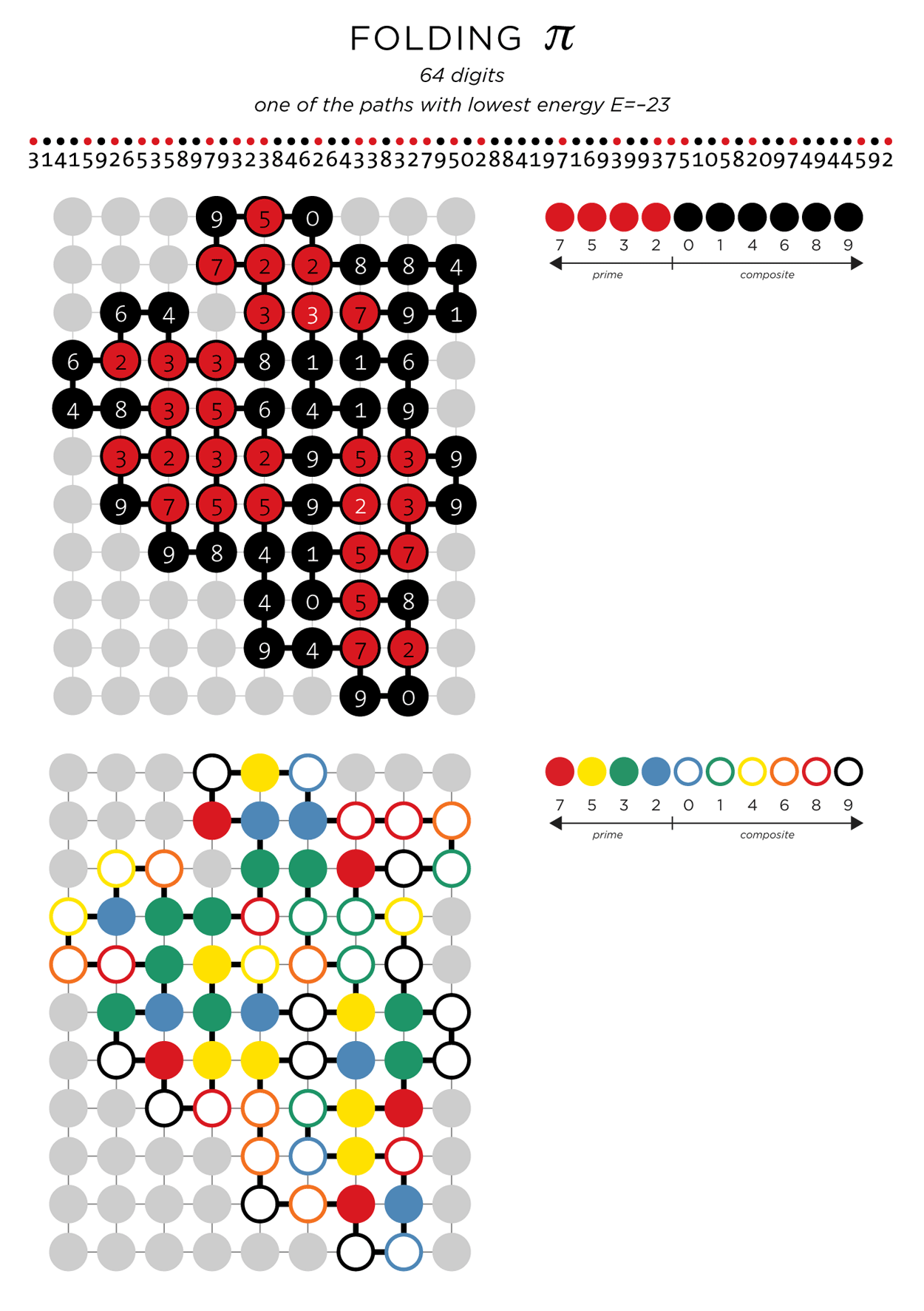
E=-23, indicating 23 neighbouring pairs. A color scheme after the Bauhaus style will be used for the art, with a different scheme for white and black backgrounds.
The quality of the path will depend on how hard you look. Each time the folding simulation is run you run the chance of finding a better solution. For the 64 digits of
π
shown above, I ran the simulation 500 times and found over 200 paths with the same low energy. It's interesting to note that the path with E=-22 was found in <1 second and it took most of the computing time to find the next move.
Below I show 100 paths of 64-digits with E=-23, sorted by their aspect ratio.

E=-23 64-digit paths — there are many more paths with this energy. The paths are in increasing order of aspect ratio (width/height). First is 6x14 (0.429) and last is 8x9 (0.889).
(zoom)
Running the simulation for 64 digits is very practical — it takes only a few minutes. In a sectino below, I show you how to run your own simulation.
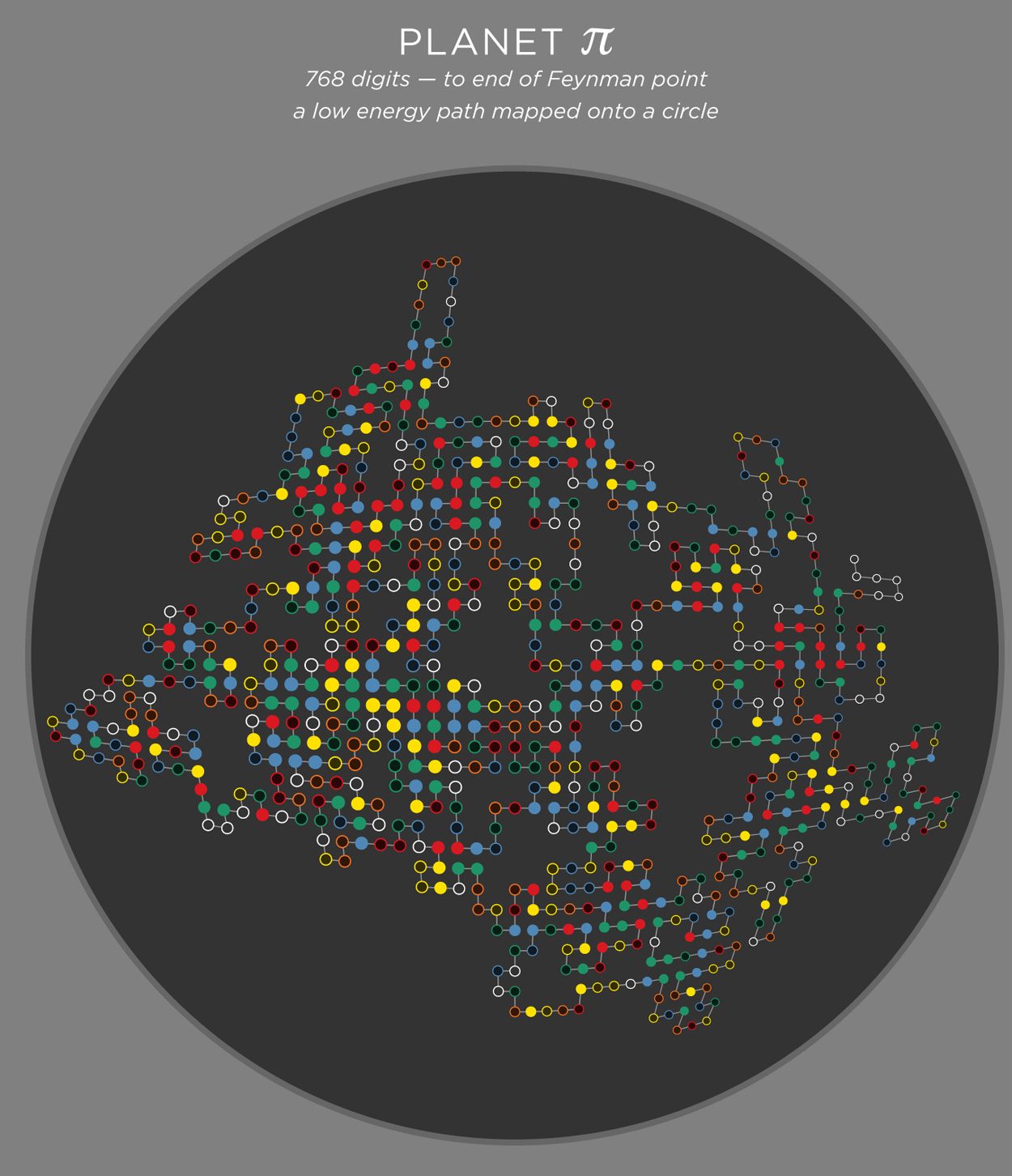
folding 768 digits of π — the Feynman Point
Let's fold more digits! How about 768 digits — all the way to "...999999". This is the famous The Feynman Point in π where we see the first set of six 9s in row. This happens surprisingly early — at digit 762. In this sequence there are 298 prime digits with the other 470 being composite.
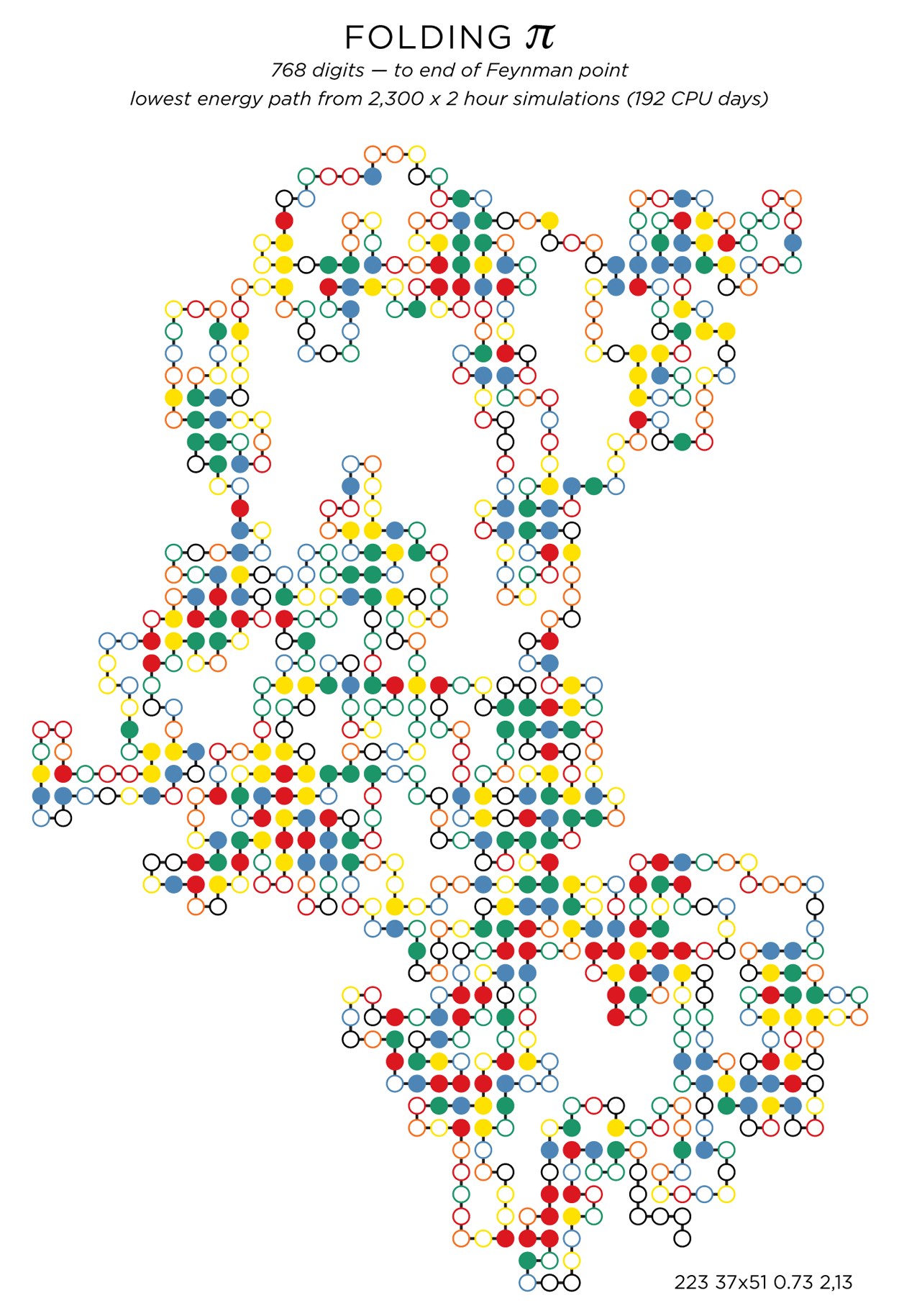
E=-223 (width=38, height=52, r=0.73, cm=1, cmabs=13).
(zoom)
I have chosen not to emphasize the start and end of the path — finding them is part of the fun (You are haven't fun, aren't you?). The end is easier to spot — the 6 9s stand out. Finding the start, on the other hand, is harder.
(d,n) points in π — sequences of repeating digits
The Feynman Point is a specific instance of repeating digits, which I call (d,n) points.
You can read more about these locations, where I have enumerated all such locations in the first 268 million digits of π .
Optimal paths of π up to Feynman Point
Below is a list of the 20 best paths that I've been able to find. They range from E=-223 to E=-219. I annotate each path with a few geometrical properties, such as width, height, area and so on. In some of the art these properties annotate the path (energy x×y r cm,cmabs).
# e - energy, as positive number # x,y - path width and height # r - aspect ratio = x/y # area - area (x*y) # cm - center of mass |(sum(x),sum(y))|/n and |(sum(|x|),sum(|y|))|/n # dend - distance between start and end of path 0 e 223 size 37 51 r 0.725 area 1887 cm 1.9 13.4 dend 24.4 1 e 222 size 36 44 r 0.818 area 1584 cm 17.3 18.8 dend 10.4 2 e 221 size 37 50 r 0.740 area 1850 cm 7.6 14.0 dend 16.3 3 e 221 size 70 36 r 1.944 area 2520 cm 1.0 17.3 dend 30.1 4 e 221 size 41 55 r 0.745 area 2255 cm 17.9 20.6 dend 29.5 5 e 221 size 50 49 r 1.020 area 2450 cm 20.8 22.1 dend 34.1 6 e 221 size 61 35 r 1.743 area 2135 cm 11.4 18.2 dend 15.0 7 e 221 size 53 45 r 1.178 area 2385 cm 14.7 18.1 dend 18.8 8 e 221 size 32 52 r 0.615 area 1664 cm 14.0 18.1 dend 33.8 9 e 220 size 46 70 r 0.657 area 3220 cm 26.6 27.8 dend 27.3 10 e 220 size 55 55 r 1.000 area 3025 cm 5.1 16.8 dend 15.0 11 e 220 size 58 34 r 1.706 area 1972 cm 9.3 14.6 dend 43.4 12 e 220 size 62 50 r 1.240 area 3100 cm 30.6 31.4 dend 33.4 13 e 220 size 41 45 r 0.911 area 1845 cm 15.4 17.6 dend 19.2 14 e 220 size 47 51 r 0.922 area 2397 cm 25.6 26.7 dend 16.0 15 e 220 size 38 52 r 0.731 area 1976 cm 13.1 15.9 dend 23.6 16 e 220 size 57 46 r 1.239 area 2622 cm 20.7 22.7 dend 51.7 17 e 220 size 43 57 r 0.754 area 2451 cm 21.3 23.3 dend 29.6 18 e 219 size 45 45 r 1.000 area 2025 cm 16.5 18.2 dend 33.1 19 e 219 size 51 46 r 1.109 area 2346 cm 16.0 19.2 dend 44.4
As you can see, the dimensions of the paths vary greatly. Low energy paths are not necessarily symmetrical. Paths with a small cm are balanced around their center. Paths with r≈1 are confined in a square boundary. Paths with small dend have their start and end points close to one another.
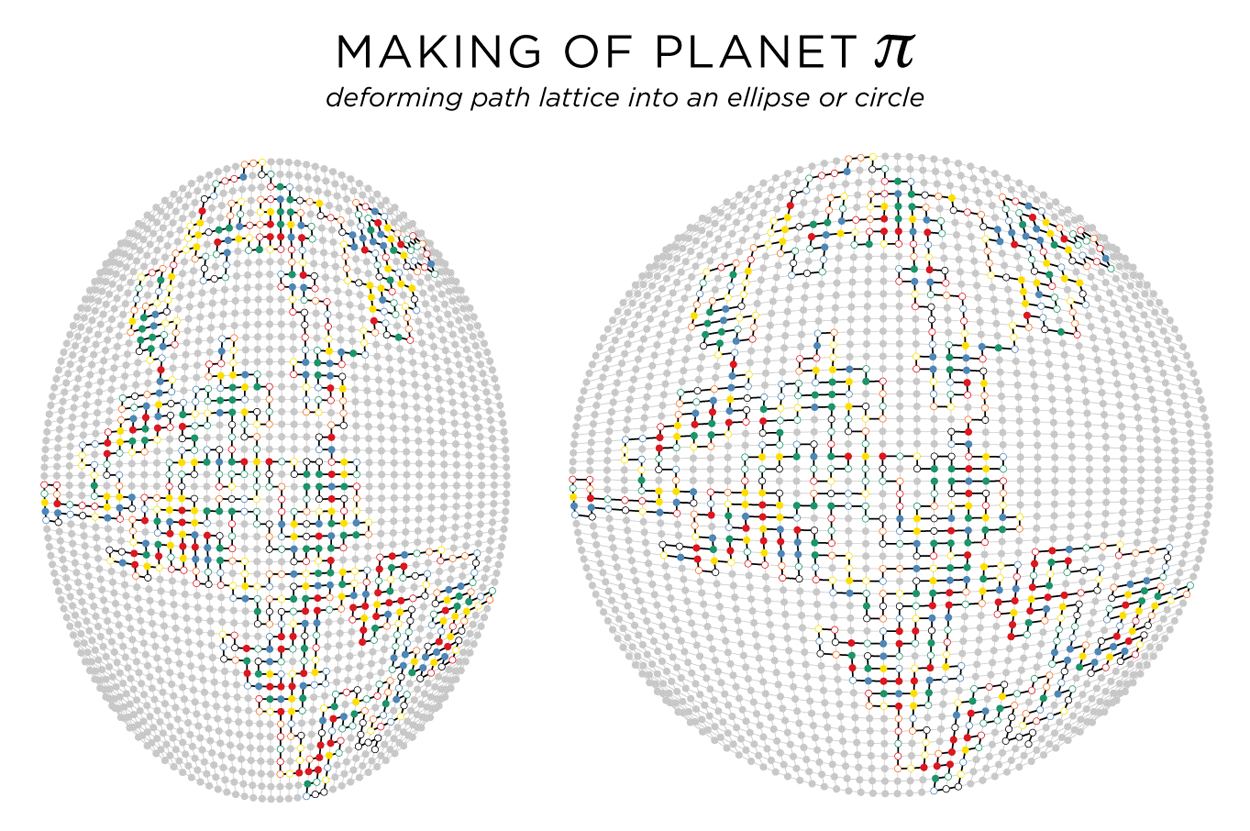
planet π — path lattice on a circle
The art would not be complete if we didn't somehow try to further force things into a circle! The path lattice is rectangular, but can be deformed into an ellipse or circle using the following transformation
` [(x'),(y')] = [(x sqrt(1-y^2/2)),(y sqrt(1-x^2/2)) ] `
Nasa to send our human genome discs to the Moon
We'd like to say a ‘cosmic hello’: mathematics, culture, palaeontology, art and science, and ... human genomes.



Comparing classifier performance with baselines
All animals are equal, but some animals are more equal than others. —George Orwell
This month, we will illustrate the importance of establishing a baseline performance level.
Baselines are typically generated independently for each dataset using very simple models. Their role is to set the minimum level of acceptable performance and help with comparing relative improvements in performance of other models.
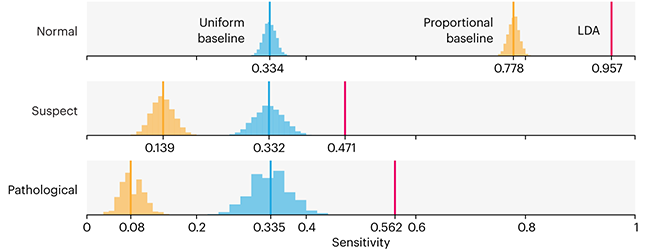
Unfortunately, baselines are often overlooked and, in the presence of a class imbalance5, must be established with care.
Megahed, F.M, Chen, Y-J., Jones-Farmer, A., Rigdon, S.E., Krzywinski, M. & Altman, N. (2024) Points of significance: Comparing classifier performance with baselines. Nat. Methods 20.
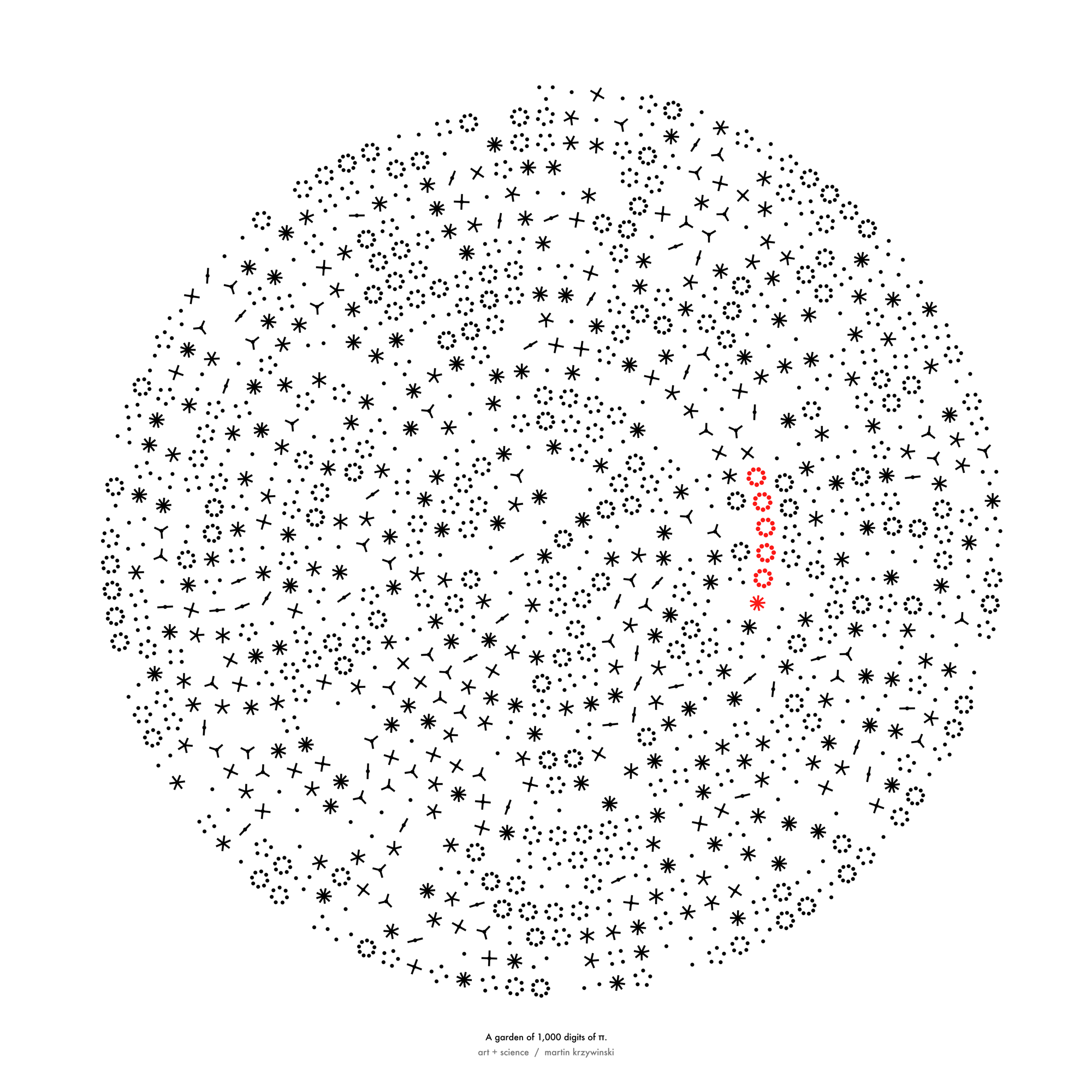
Happy 2024 π Day—
sunflowers ho!
Celebrate π Day (March 14th) and dig into the digit garden. Let's grow something.
How Analyzing Cosmic Nothing Might Explain Everything
Huge empty areas of the universe called voids could help solve the greatest mysteries in the cosmos.
My graphic accompanying How Analyzing Cosmic Nothing Might Explain Everything in the January 2024 issue of Scientific American depicts the entire Universe in a two-page spread — full of nothing.
The graphic uses the latest data from SDSS 12 and is an update to my Superclusters and Voids poster.
Michael Lemonick (editor) explains on the graphic:
“Regions of relatively empty space called cosmic voids are everywhere in the universe, and scientists believe studying their size, shape and spread across the cosmos could help them understand dark matter, dark energy and other big mysteries.
To use voids in this way, astronomers must map these regions in detail—a project that is just beginning.
Shown here are voids discovered by the Sloan Digital Sky Survey (SDSS), along with a selection of 16 previously named voids. Scientists expect voids to be evenly distributed throughout space—the lack of voids in some regions on the globe simply reflects SDSS’s sky coverage.”
voids
Sofia Contarini, Alice Pisani, Nico Hamaus, Federico Marulli Lauro Moscardini & Marco Baldi (2023) Cosmological Constraints from the BOSS DR12 Void Size Function Astrophysical Journal 953:46.
Nico Hamaus, Alice Pisani, Jin-Ah Choi, Guilhem Lavaux, Benjamin D. Wandelt & Jochen Weller (2020) Journal of Cosmology and Astroparticle Physics 2020:023.
Sloan Digital Sky Survey Data Release 12
Alan MacRobert (Sky & Telescope), Paulina Rowicka/Martin Krzywinski (revisions & Microscopium)
Hoffleit & Warren Jr. (1991) The Bright Star Catalog, 5th Revised Edition (Preliminary Version).
H0 = 67.4 km/(Mpc·s), Ωm = 0.315, Ωv = 0.685. Planck collaboration Planck 2018 results. VI. Cosmological parameters (2018).
constellation figures
stars
cosmology
Error in predictor variables
It is the mark of an educated mind to rest satisfied with the degree of precision that the nature of the subject admits and not to seek exactness where only an approximation is possible. —Aristotle
In regression, the predictors are (typically) assumed to have known values that are measured without error.
Practically, however, predictors are often measured with error. This has a profound (but predictable) effect on the estimates of relationships among variables – the so-called “error in variables” problem.
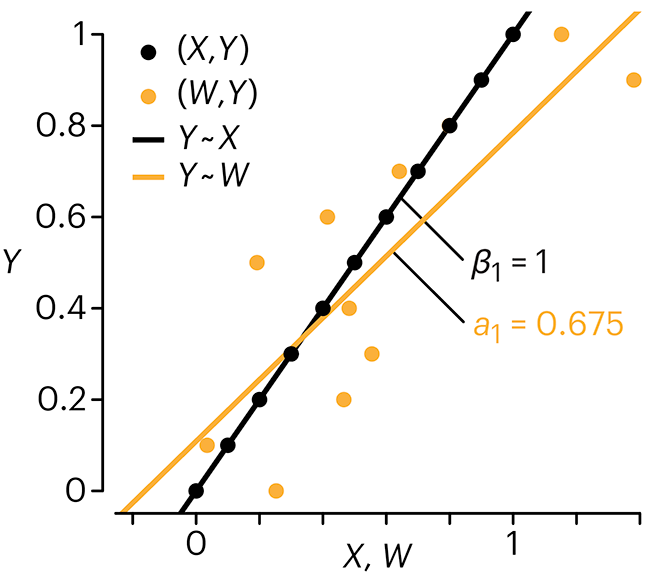
Error in measuring the predictors is often ignored. In this column, we discuss when ignoring this error is harmless and when it can lead to large bias that can leads us to miss important effects.
Altman, N. & Krzywinski, M. (2024) Points of significance: Error in predictor variables. Nat. Methods 20.
Background reading
Altman, N. & Krzywinski, M. (2015) Points of significance: Simple linear regression. Nat. Methods 12:999–1000.
Lever, J., Krzywinski, M. & Altman, N. (2016) Points of significance: Logistic regression. Nat. Methods 13:541–542 (2016).
Das, K., Krzywinski, M. & Altman, N. (2019) Points of significance: Quantile regression. Nat. Methods 16:451–452.
Convolutional neural networks
Nature uses only the longest threads to weave her patterns, so that each small piece of her fabric reveals the organization of the entire tapestry. – Richard Feynman
Following up on our Neural network primer column, this month we explore a different kind of network architecture: a convolutional network.
The convolutional network replaces the hidden layer of a fully connected network (FCN) with one or more filters (a kind of neuron that looks at the input within a narrow window).
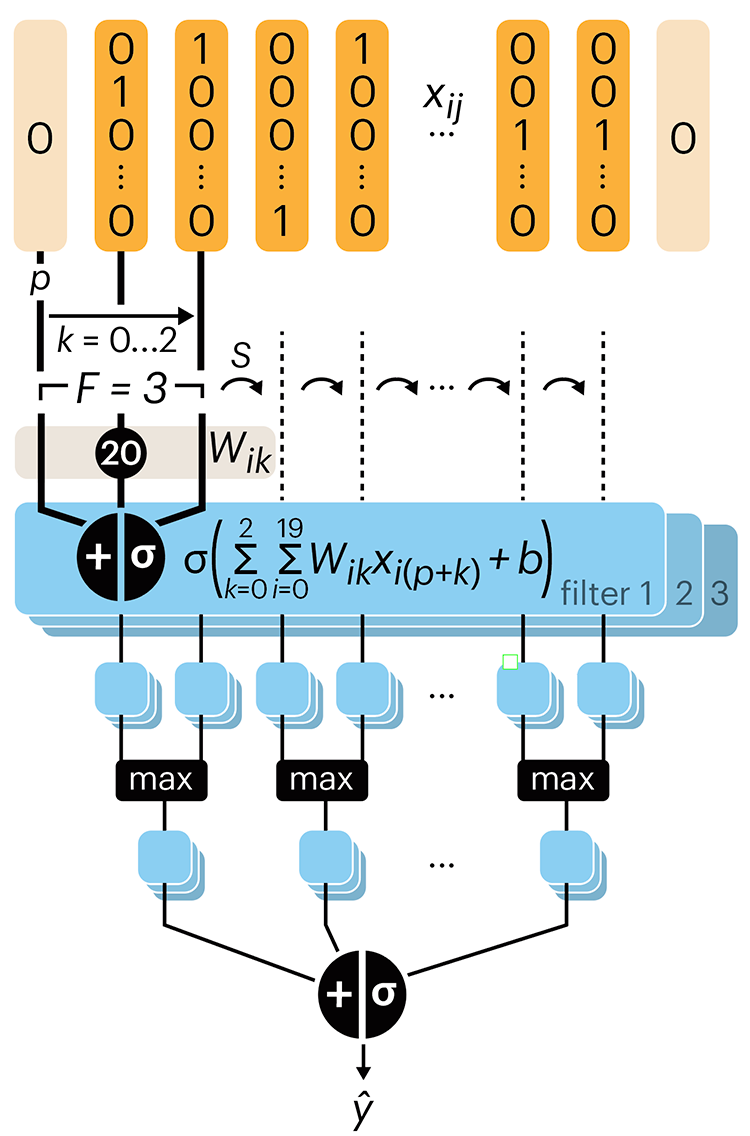
Even through convolutional networks have far fewer neurons that an FCN, they can perform substantially better for certain kinds of problems, such as sequence motif detection.
Derry, A., Krzywinski, M & Altman, N. (2023) Points of significance: Convolutional neural networks. Nature Methods 20:1269–1270.
Background reading
Derry, A., Krzywinski, M. & Altman, N. (2023) Points of significance: Neural network primer. Nature Methods 20:165–167.
Lever, J., Krzywinski, M. & Altman, N. (2016) Points of significance: Logistic regression. Nature Methods 13:541–542.