Max Cooper's Ascent — Making of the Music video
Enter the 5th dimension
contents
The scene takes place on a 5-dimensional stage, which is projected onto two dimensions (without perspective). Over time, cubes appear on the stage. Throughout the video, both the camera and each cube can rotate independently.
For some cubes, area maps of the digits of `\pi` or its approximations (e.g. 22/7) are projected onto some of the faces of the cube.
The video was created with a custom animation system that I wrote specifically for Ascent.
The animation is structured around a series of keyframes. Each keyframe (there are about 170 keyframes) is defined using a custom scripting language with which I can add elements to the scene, apply a rotation, zoom and scale, project area maps, and so on.
The keyframes were created manually and the motion was designed to match the dynamics and movement of the music. There is no automated synchronization.
For example, the first 8 seconds of the video is created from these keyframe definitions.
# parameter definitions ... param = fs 24 # angle in units of 2π (–17.6 deg) param = astepa2 d-0.048978 ... # add a cube with size 0 and edge fade 1 frame = 1.a; cube_add(c0,0,1) # rotate the scene in yw plane by 'astepa2' amount (defined elsewhere) frame = 1.a0; a yw astepa2 # previous keyframe parameters will be interpolated over # 2fs = 48 frames (2 seconds at 24 fps) to values of the next keyframe # i.e. cube c0 edge fade in xy plane will linearly decrease from 1 to 0 frame = 1.a1; n 2fs; c c0 f [xy] 0 # cube c0 x size grows to 0.05 frame = 1.a2; n 2fs; c c0 s [x] 0.05 # cube c0 x size grows to 0.10 frame = 1.a3; n 2fs; c c0 s [x] 0.10 # cube c0 x size grows to 0.15 frame = 1.a4; n 2fs; c c0 s [x] 0.15 ...
Here are the first four keyframes — there are 2fs = 48 interpolated frames between each of these keyframes.

c c0 f [xy] 0

c c0 f [xy] 0
c c0 s [x] 0.05

c c0 s [x] 0.05
c c0 s [x] 0.10

c c0 s [x] 0.10
c c0 s [x] 0.15
For all the keyframes, see the keyframe section.
The 5-cube (`n=5`) has `2^5=32` vertices (0-cubes, corners), `2^4 \times 5 = 80` edges (1-cubes, lines), `2^3 \times 10 = 80` faces (2-cubes, squares), `2^2 \times 10 = 40` cubic cells (3-cubes) and `2^1 \times 5 = 10` tesseract cells (4-cubes).
In general, the number of `m`-cubes in an `n`-cube is $$E_{m,n} = 2^{n-m} \binom{n}m $$
Here's a sample frame from the video — this is frame 830/8520.
It shows a pair of three dimensional cubes, each with lines growing from their vertex towards the other cube.
But what you're actually seeing is a single 5 dimensional cube, but with some dimensions collapsed and edges along other dimensions not fully drawn.

a xw astepb4
c c0 f [w] 0.9
c c0 s [w] 0.715
c c0 s [xyz] 0.15
rots
rxy2
!ryz2
a xw astepb4
c c0 f [w] 0.8
c c0 s [w] 0.615
c c0 s [xyz] 0.15
rots
rxy2
!ryz2
The view table shows the camera zoom and angle (in degrees). In 2-dimensional space there is one direction of rotation — in the `xy` plane (axis of rotation is `z`). In 3-dimensional space, there are three directions of rotation — in the `xy`, `yz` and `xz` planes. Once we reach 5 dimensions there are 10 directions of rotation (`xy`, `yz`, `xw`, `xv`, `yz`, `yw`, `yv`, `zw, `zv, `wv`).
In this frame, 7 of these angles are non-zero. It's essentially impossible to look at these angles and be able to predict how the rotated cube will look. To explore rotations in 4-dimensional space, check out Bartosz Chechanowski's excellent article on Tesseract building and rotation.
Each cube has its own angles. In this frame, the cube's angles are all zero, meaning that the rotation in the scene is due entirely to the rotation of the camera. Once more cubes are introduced, each can rotate independently to make the animation more dynamic.
There is one 5-dimensional cube in this scene (C0) and its size, edge length and rotation is presented in another table.
The cube has 5 size values, which correspond how far the cube extends into each of the dimensions. If the size `s_d` is zero then dimension `d` is collapsed. For example, if `s_w = s_v = 0` and `s_x = s_y = s_z = 1` then we just have a regular 3-cube.
In this frame, the cube has grown quite a bit in the 4th dimension `s_w = 0.64` but not as much in the first three dimensions `s_x = s_y = s_z = 0.15`. The fifth dimension is collapsed `s_v = 0`.
The cube's edge values `e_d` indicate how much of the edge along that dimension is drawn. If `e_d = 1` then the edge spans the full distance between vertices. For fractional values, the edge will extend only partially from the corner along the distance.
In this frame, the edges in the first three dimensions are fully drawn but along `w` the edge value is `e_w = 0.18` — the middle 82% of the edge is not drawn.
The combination of size and edge values can highlight lower-dimensional components of the cube — for example, by not drawing edges along certain dimension.

a xw astepb4
c c0 f [w] 0.2
c c0 s [w] 0.215
rots
rxy2
!ryz2
a xw astepb4
c c0 f [w] 0.0
c c0 s [w] 0.150
rots
rxy2
!ryz2
By the time we get to frame 1050, the edges along the `w` dimension are almost completely drawn (`e_w = 0.87`). But also the size of the cube along `w` has shrunk from `s_w = 0.64` to 0.19, which is very close to the size of the cube in the other dimensions (`s_{xyz} = 0.15`). This has the effect of bringing the 3-cube cells closer together.

c c0 f [v] 0.80
c c0 s [xyzwv] 0.250
rots
rxy2
ryz2
c c0 f [v] 0.70
c c0 s [xyzwv] 0.275
rots
rxy2
ryz2
Shortly after, the cube's `v` dimension has grown (now the size along all dimensions is the same, `s_{xyzwv} = 0.25`) and edges are starting to form along the `v` dimension (`e_v` = 0.21).

c c0 f [v] 0.10
rots
rxy2
ryz2
c c0 f [v] 0.00
rots
rxy2
ryz2
And, finally at frame 1726, we have our first complete (`s_{xyzwv} = e_{xyzwv} = 1`) 5-dimensional cube.
You now have everything that you need to interpret the full video. So, let's gets started on the walkthrough.
The walkthrough takes you through interesting landmarks in the video. It shows the frame, the keyframe before and after the frame (the frame is interpolated between these) and the parameters (size, edge, rotation, etc) of each object in the frame.
For a full list of keyframes, see the keyframe section.
Initially the scene is blank — we have one cube but its size in all dimensions is zero.

c c0 f [xy] 0
Slowly, the cube's size in the `x` dimension grows, now at `s_x = 0.14`. Edge values are `e_x = e_y = 1` meaning that the edge is completely drawn between vertices. The edge appears to grow because it's the cube that is growing (`s_x` is increasing).

c c0 s [x] 0.10
c c0 s [x] 0.15
The cube has grown to `s_x = 0.15` and is now growing in the `y` dimension (`s_y = 0.07`). Simultaneously, the scene is rotating in the `xy` plane. Note that there is an initial non-zero `yw` plane angle — this sets us up for an interesting point of view for when we start seeing the `w` dimension.

c c0 s [y] 0.05
rxy3
c c0 s [y] 0.10
rxy3
Next, the `z` diemension grows and we're finally starting to see a 3-cube form. We perceive two 2-cubes (squares) splitting up, with edges forming between them (`e_z = 0.85`). Of course, what's actually happening is that the 3-cube's `z` dimension is growing.

c c0 f [z] 0.20
c c0 s [xy] 0.15
c c0 s [z] 0.130
ryz6
c c0 f [z] 0.10
c c0 s [xy] 0.15
c c0 s [z] 0.140
ryz6
Around frame 675 is the first time we get a hint of higher dimensions. By now, the cube has grown equally in the first three dimensions (`s_{xyz} = 0.15`) and edges along these dimensions are fully formed (`e_{xyz} = 1`).
The cube now appears to be splitting into two copies because its `w` dimension is growing (`s_w = 0.12`). But, because no edges are drawn along this dimension (`e_w = 0`), the cubes don't appear to be connected in any way. Thus, we still really don't know how many dimensions this scene has — the effect is the same as if we were looking at a 3-dimensional scene in which a 3-cube splits into two.

c c0 f [z] 0.00
c c0 s [xy] 0.15
c c0 s [z] 0.150
ryz6
c c0 s [w] 0.815
c c0 s [xyz] 0.15
At frame 730, it looks like we have a pretty symmetric stacking of two 3-cubes but we're actually looking at a 4-cube without `w` edges and rotated in the `xy`, `yz` and `yw` planes to achieve this effect.

c c0 s [w] 0.815
c c0 s [xyz] 0.15
The scene now starts to rotate in a more complex fashion and edges along the `w` dimension begin to grow (`e_w = 0.07`) as this dimension starts to shrink (`e_w=0.74`) to the same size as (`e_{xyz} = 0.15`).

a xw astepb4
c c0 f [w] 0.9
c c0 s [w] 0.715
c c0 s [xyz] 0.15
rots
rxy2
!ryz2
This process continues and by frame 1500, the cube's size in all dimenions is the same (`e_{xyzwv} = 0.31`) and only the edges along `v` still need to grow to completion (right now, they're about 50% extended).

c c0 f [v] 0.50
c c0 s [xyzwv] 0.300
rots
rxy2
ryz2
c c0 f [v] 0.40
c c0 s [xyzwv] 0.325
rots
rxy2
ryz2
By now, the entire scene has zoomed in a little bit — the camera zoom has increased from 1 to 1.3.
Finally, more interesting things begin to happen. Four new cubes are introduced (C1, C2, C3, C4). Initially, these have the same size in each dimension as our original cube C0, but their `e_{xyzwv} = 0`, so no edges are drawn.
Then, the edges for C1 start to grow. Initially, only in the `xy` plane (`e_{xy} = 0.36)`. These edges are drawn with a thicker line and a difference blend, so what you're seeing (in the black and white version) is something that looks like a tube growing from the vertices.
The purpose of this scene is to draw attention to the faces in the `xy` plane.

c c1 f [xy] s2f
rotthis2
c c1 f [xy] s2f
rotthis2
As the edges in C1 continue to grow, the edges in C2 in the `xz` plane start to grow (`e_{xz} = 0.46`).

c c1 f [xy] s2f
c c2 f [xz] s2f
rotthis2
c c1 f [xy] s2f
c c2 f [xz] s2f
rotthis2
Finally, each of the C1–C4 cubes has grown its edges fully: C1 in `xy`, C2 in `xz`, C3 in `xw` and C4 in `xv`.
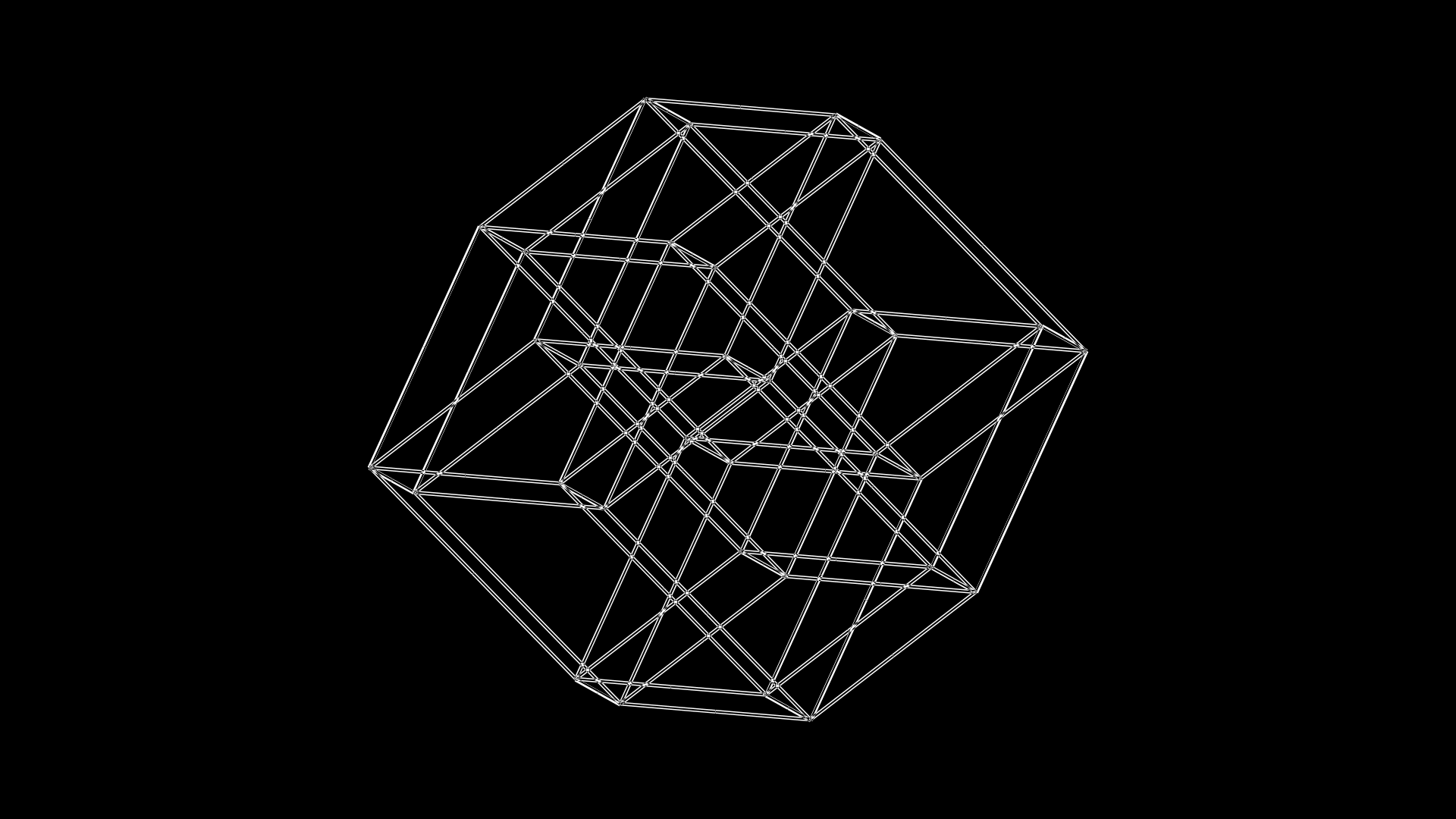
c c1 f [xy] s2f
c c2 f [xz] s2f
c c3 f [xw] s2f
c c4 f [xv] s2f
rotthis2
c c1 f [xy] 0
c c2 f [xz] 0
c c3 f [xw] 0
c c4 f [xv] 0
rotthis2
Now, something funky starts to happen. It looks like the faces from the original C0 cube are coming off. Yes they are.
This is achieved by increasing the size of the cubes C1–C4, which, if you remember, only had edges drawn within one plane (e.g. `xy`).
In this frame, cube C1 has grown from `s_{xyzwv} = 0.33` to 0.38. This is the cube that has `xy` edges (`e_x = e_y = 1`).
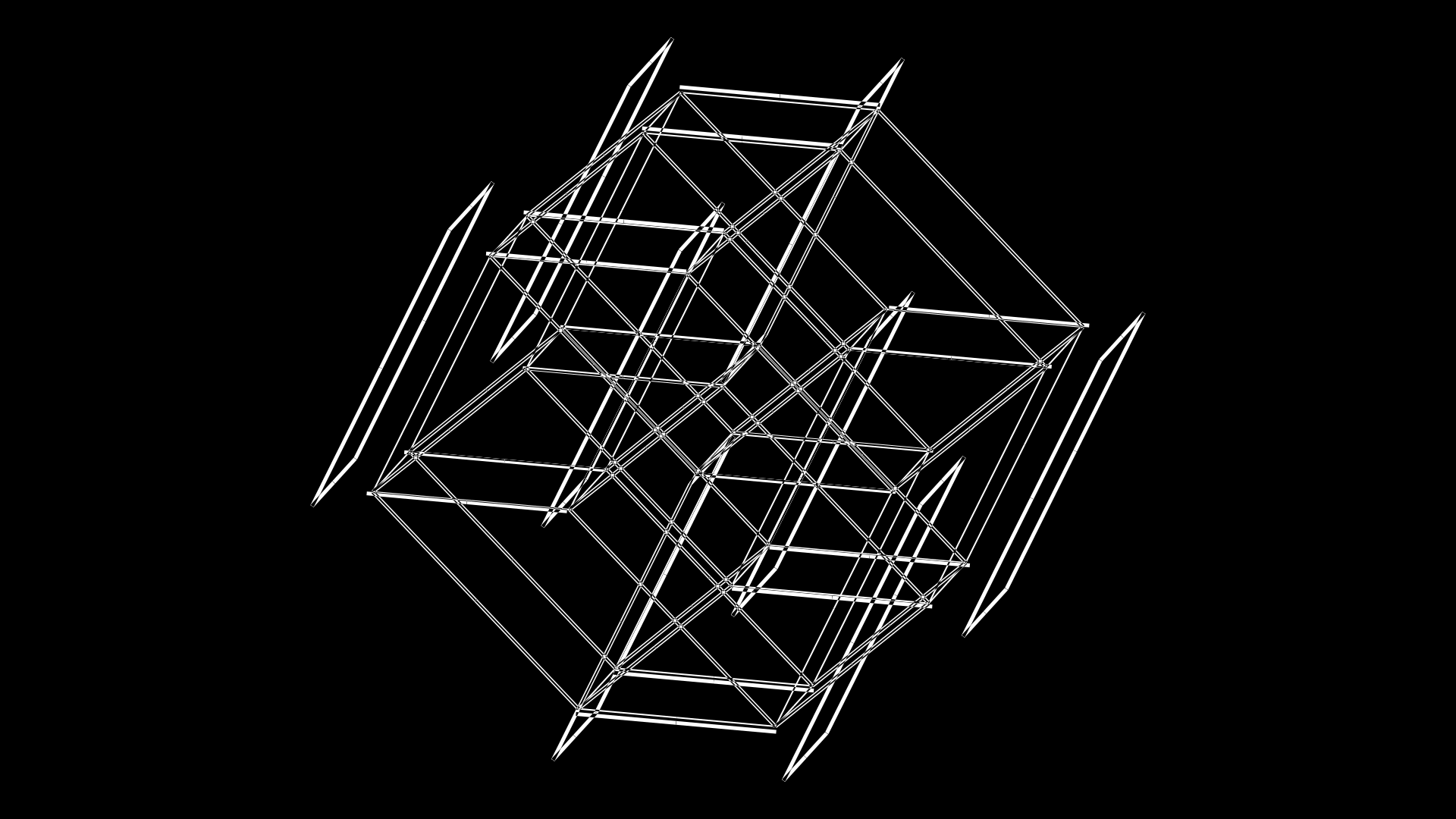
c c1 s . s3s
rotthis2
c c1 s . s3s
c c2 s . s3s
rotthis2
Now, quite a bit is happening but it can all be understood in terms of what you've already seen.
First, the C1–C4 cubes have grown (each to a different extent) beyond the size of C0 (which makes their faces look like they've separated). For example, C1 has `s = 0.54` whereas C4 grew less at `s = 0.39`.
The other effect is that the edges for C0 are now shrinking towards the cube's vertices — this achieved by lowering the edge size to `e = 0.55`.
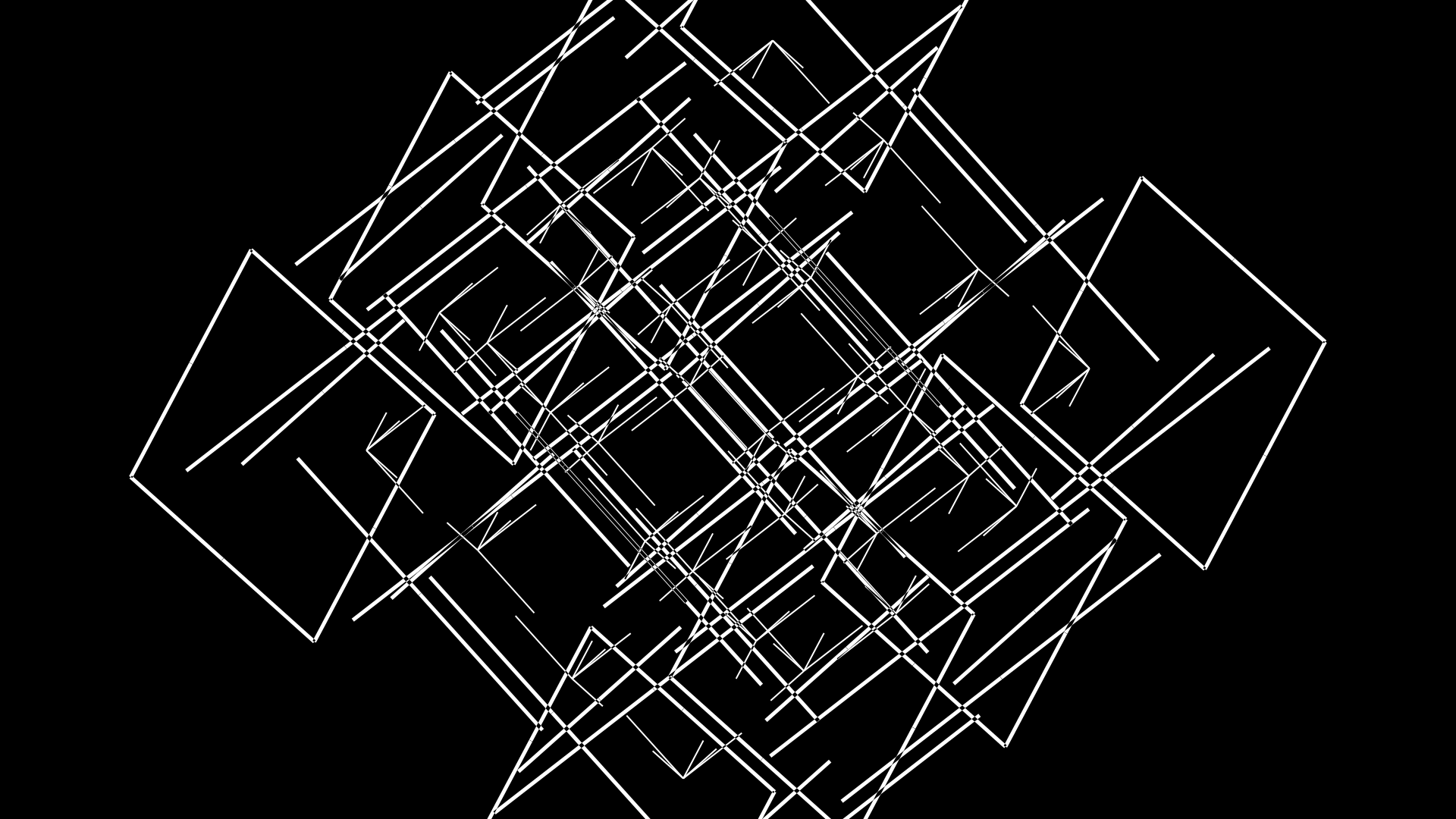
c c0 f . s3f
c c[1-4] s . s3s
rotthis2
c c0 f . s3f
c c[1-4] s . s3s
rotthis2
rep 2
Ready for more? Yes you are.
The edges of C0 have shrunk back to the cube's vertices (`e = 0.18`) so we only see 18% of the total edge length (i.e. there is a 82% gap in the middle of the edge). You'll also notice that the edges of C1 are starting to shrink (`e = 0.94`), which you can see as a small gap forming in one set of the thicker squares (e.g. first face from the right of the frame).
You're also seeing little specks form everywhere. These are the beginnings of the area maps of the digits of `\pi` (or its approximations), projected onto the faces of a cube.

c c0 f . 0.90
c c1 f [xy] s4f
c c[0-1] s . p2
map_fade(c1,.,p1)
rotthis3
size . s4u
`e` = 0.01 `z` = 1.00
`e` = 0.00 `z` = 1.00
`e` = 0.00 `z` = 1.00
`e` = 0.00 `z` = 1.00
In this frame, I've assigned maps to each of the 80 faces of cubes C1–C4. That's 300 maps. The map name reflects the digit and the levels of the map. For example, map 22a is a 2-level map of the `22/7` approximation and 22b is a 3-level version of it.
map = 10a 10/3 2 map = 10b 10/3 3 map = 10c 10/3 4 map = 22a 22/7 2 map = 22b 22/7 3 map = 22c 22/7 4 map = 179a 179/57 2 map = 179b 179/57 3 map = 179c 179/57 4 map = 245a 245/78 2 map = 245b 245/78 3 map = 245c 245/78 4 map = 355a 355/113 2 map = 355b 355/113 3 map = 355c 355/113 4 map = pia pi 2 map = pib pi 3 map = pic pi 4
The scene keeps zooming in — now the zoom is `z = 2`. Cube C0 keeps growing `s = 0.67` and its edges continue to fade to the corners `e = 0.1`. Cubes C1–C4 keep growing and the edges of the maps on their faces are also growing. For example, cube's C1 and C2 maps have `e=0.10`.

a xv 0.10
a xw 0.90
a xz 0.16
c c2 f [xz] s4f
c c[0-2] s . p2
cube c[1-2] a [xy][yzwvu] astep-fast
map_fade(c2,.,p1)
rotthis3
size . s4u
a yv 0.15
a yw 0.03
c c3 f [xw] s4f
c c[0-3] s . p2
cube c[1-2] a [xy][yzwvu] astep-fast
map_fade(c3,.,p1)
rotthis3
size . s4u
`e` = 0.10 `z` = 1.00
`e` = 0.10 `z` = 1.00
`e` = 0.04 `z` = 1.00
`e` = 0.00 `z` = 1.00
The scene continues to zoom (`z=2.59`) and the edges of all cubes have faded to corners (`e = 0.1`). The map edges are around 20% complete.
Because the scene zoomed in quite a bit now, you don't see all the corners of any given cube. Periodically, corners fly by and then quickly pass out of view.

c c4 f [xv] s4f
cube c[1-4] a [xy][yzwvu] astep-fast
map_fade(c[1-4],.,p1)
rotthis3
size . s4u
cube c[1-4] a [xy][yzwvu] astep-fast
map_fade(c[1-4],.,p1)
rotthis3
size . s4u
`e` = 0.22 `z` = 1.00
`e` = 0.22 `z` = 1.00
`e` = 0.19 `z` = 1.00
`e` = 0.16 `z` = 1.00
At this point, four more cubes are introduced into the scene: C5–C8. These cubes are different from the cubes we've already seen in that instead of shown as edges, they are shown as filled faces. Faces may be incompletely drawn (i.e. not the full face but only as square patches near their vertices.
The faces of cubes C5 and C6 are partially drawn (`e=0.16` and `e=0.09`, respectively). Faces for cubes C7 and C8 are not yet drawn (`e=0`).

c c[1-4] a [xy][yzwvu] astep-vfast
c c[5-5] f . s5cf
map_fade(c[1-4],.,s5f)
rotthis3
c c[1-5] a [xy][yzwvu] astep-vfast
c c[5-6] f . s5cf
map_fade(c[1-4],.,s5f)
rotthis3
rep 5
`e` = 0.20 `z` = 1.00
`e` = 0.20 `z` = 1.00
`e` = 0.17 `z` = 1.00
`e` = 0.14 `z` = 1.00
By now, the faces for each cube C5–C8 are being drawn (`e>0`). From this angle, the corners of these cubes are at the periphery of the viewport. At the same time, the projected area maps on cubes C1–C4 start to fade away (maps' `e` is decreasing).
Notice that each of the cubes C1–C8 has its own rotation, in addition to the rotation of the camera.

c c[1-6] a [xy][yzwvu] astep-vfast
c c[5-7] f . s5cf
map_fade(c[1-4],.,s5f)
rotthis3
rep 9
c c[1-7] a [xy][yzwvu] astep-vfast
c c[5-8] f . s5cf
map_fade(c[1-4],.,s5f)
rotthis3
rep 4
`e` = 0.07 `z` = 1.00
`e` = 0.07 `z` = 1.00
`e` = 0.04 `z` = 1.00
`e` = 0.01 `z` = 1.00
Cube faces continue to grow and as they do so, there's more of a chance that the viewport is filled with them. The area maps are almost entirely gone.

c c[1-8] a [xy][yzwvu] astep-vfast
c c[5-8] f . s5cs
rotthis3
rep 5
`e` = 0.04 `z` = 1.00
`e` = 0.04 `z` = 1.00
`e` = 0.01 `z` = 1.00
`e` = 0.00 `z` = 1.00
The Ascent video released as a black-and-white version, which is the source of the frames you've seen in this walkthrough.
There are two more versions of the video — one using the viridis (yellow, green, blue, purple) color scheme and the other using plasma (yellow, orange, red, pruple, violet).
The color encodes the z-distance (into the screen) to the element.


At around 4 minutes into the video, the entire scene appears to reset. This is achieved by slowly resetting the scene angle to a specific point of view — don't ask me how long it took to find it.






The angles of all cubes are either zero or 180 and the scene is rotated so that what we see is a pretty minimal projection.
You'll notice that 5 new cubes Ca—Cd have been introduced. These have maps for 22/7 and 179/57, which are starting to grow. The elements for these maps are drawn as filled rectangles instead of just outlines.

a xv refxv
a xw refxw
a xy refxy
a xz refxz
a yv refyv
a yw refyw
a yz refyz
c c[0-9a-d] a . 0
map_fade(c[a-d],.,ps6)
a xw d0.01
cube c[0-8] fade . ps15
cube_rot(.,[xy][yzwvu],astep-vvslow)
f . . map . fade ps15
rot6vvs
size . ps20
`e` = 0.04 `z` = 1.00
`e` = 0.04 `z` = 1.00
`e` = 0.01 `z` = 1.00
`e` = 0.00 `z` = 1.00
`e` = 0.01 `z` = 1.00
`e` = 0.01 `z` = 1.00
`e` = 0.01 `z` = 1.00
`e` = 0.01 `z` = 1.00
The scene starts to unravel and the rectangles of the area maps start to look like falling snow.






This part of the video looks particularly warm and inviting when rendered in color.


The last 4 cubes are introduced: Ce–Ch. These have area maps of the digits of `\pi`, which are also drawn as filled rectangles. Notice that when a cube's edge parameter is zero `e = 0` the cube itself isn't drawn but area map projections on its faces can appear if the maps' `e>0`.

cube c[0-2] fade . p5
cube_rot(.,[xy][yzwvu],astep-med)
face c[0-9a-e] . map . fade p5
rot6f
rep 2
`e` = 0.06 `z` = 1.00
`e` = 0.06 `z` = 1.00
`e` = 0.03 `z` = 1.00
`e` = 0.02 `z` = 1.00
`e` = 0.03 `z` = 1.00
`e` = 0.03 `z` = 1.00
`e` = 0.03 `z` = 1.00
`e` = 0.03 `z` = 1.00
`e` = 0.02 `z` = 1.00
`e` = 0.00 `z` = 1.00
`e` = 0.00 `z` = 1.00
`e` = 0.00 `z` = 1.00
For the climax, everything that's been seen so far is turned back on: edges grow, cube faces are filled and all map edges and filled rectangles grow. All the elements are rendered with difference blend (i.e. black on black gives white, white on white gives black) and the scene turns to noise.






The noise builds and you get brief glimpses of thousands of edges and faces stacking into vague patterns. If you look at the cube parameters for this frame 7440, you'll notice that everything is “on”: Cubes C0–C8 have a non-zero size and non-zero edge and the remaining cubes have map edges in the interval `e = [0.18,0.41]`.

cube_rot(.,[xy][yzwvu],astep-med)
rot6vf
rep 2
`e` = 0.43 `z` = 1.00
`e` = 0.43 `z` = 1.00
`e` = 0.41 `z` = 1.00
`e` = 0.40 `z` = 1.00
`e` = 0.41 `z` = 1.00
`e` = 0.41 `z` = 1.00
`e` = 0.41 `z` = 1.00
`e` = 0.41 `z` = 1.00
`e` = 0.40 `z` = 1.00
`e` = 0.34 `z` = 1.00
`e` = 0.27 `z` = 1.00
`e` = 0.18 `z` = 1.00
By about 5:20, it's time to wrap the show up. This is done by slowly zooming the camera out and shrinking the edges of all cubes and maps.






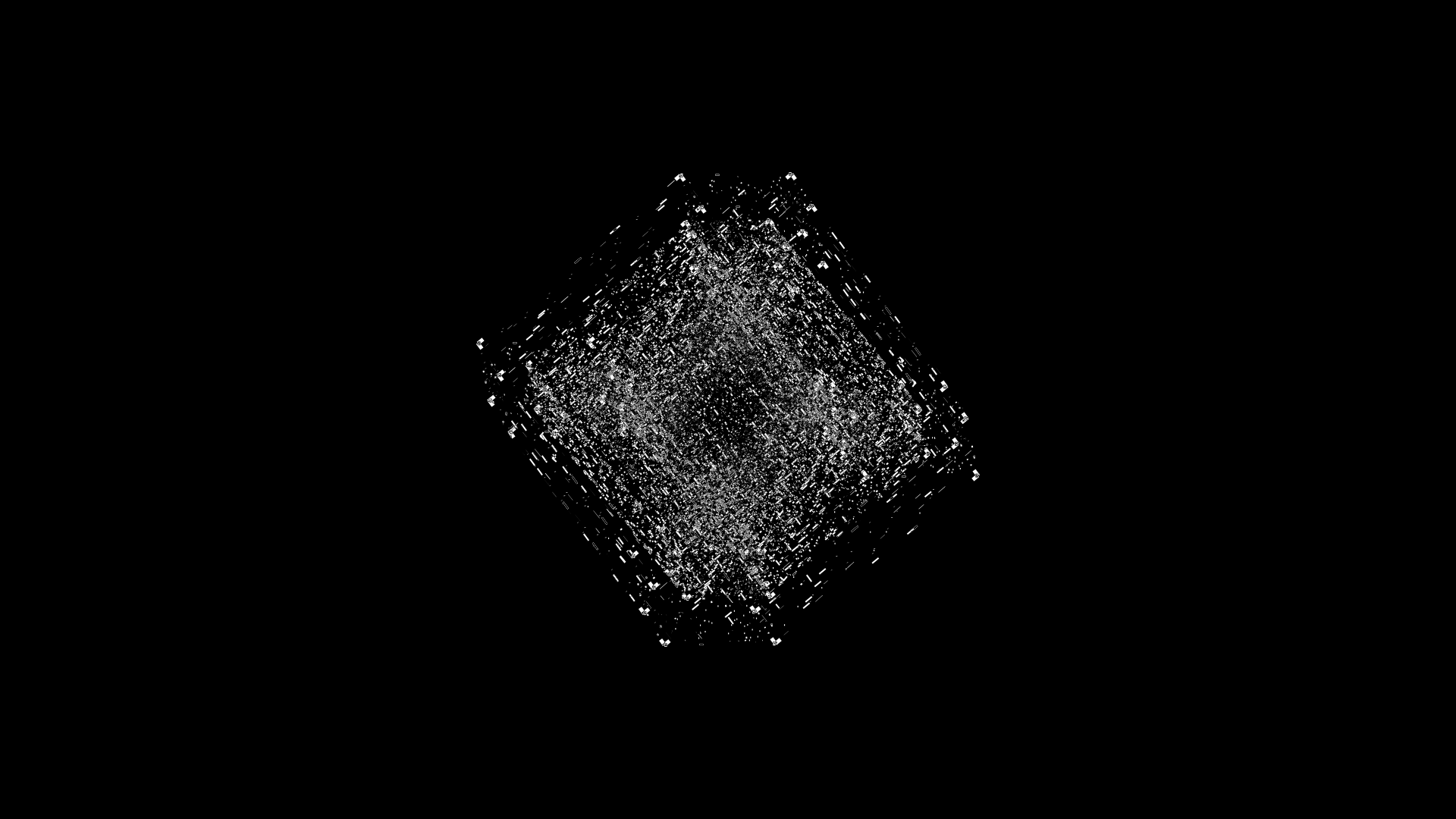

In the color versions of the video, the zoomout gives you a chance to see more details.


In this frame, one of the last where anything is visible, the zoom is `z=0.25` and cube edges are `e<0.03` and the maps have disappeared (`e=0`). Thus, what you're seeing is just the `3 \times 32 = 96` tiny vertices of cubes C0, C1 and C2.

cube . f . q50
cube_rot(.,[xy][ywvu],astep-med)
map_fade(.,.,q50)
rot6s
size . q30
rep 6
`e` = 0.00 `z` = 1.00
`e` = 0.00 `z` = 1.00
`e` = 0.00 `z` = 1.00
`e` = 0.00 `z` = 1.00
`e` = 0.00 `z` = 1.00
`e` = 0.00 `z` = 1.00
`e` = 0.00 `z` = 1.00
`e` = 0.00 `z` = 1.00
`e` = 0.00 `z` = 1.00
`e` = 0.00 `z` = 1.00
`e` = 0.00 `z` = 1.00
`e` = 0.00 `z` = 1.00
A second later, everything is gone.
Nasa to send our human genome discs to the Moon
We'd like to say a ‘cosmic hello’: mathematics, culture, palaeontology, art and science, and ... human genomes.



Comparing classifier performance with baselines
All animals are equal, but some animals are more equal than others. —George Orwell
This month, we will illustrate the importance of establishing a baseline performance level.
Baselines are typically generated independently for each dataset using very simple models. Their role is to set the minimum level of acceptable performance and help with comparing relative improvements in performance of other models.
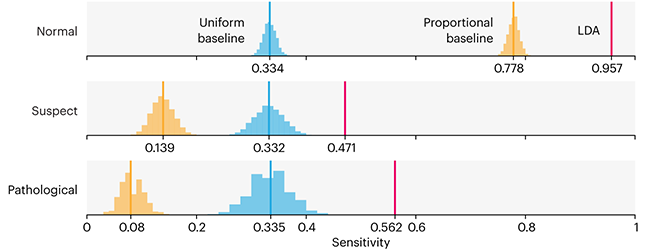
Unfortunately, baselines are often overlooked and, in the presence of a class imbalance5, must be established with care.
Megahed, F.M, Chen, Y-J., Jones-Farmer, A., Rigdon, S.E., Krzywinski, M. & Altman, N. (2024) Points of significance: Comparing classifier performance with baselines. Nat. Methods 20.
Happy 2024 π Day—
sunflowers ho!
Celebrate π Day (March 14th) and dig into the digit garden. Let's grow something.
How Analyzing Cosmic Nothing Might Explain Everything
Huge empty areas of the universe called voids could help solve the greatest mysteries in the cosmos.
My graphic accompanying How Analyzing Cosmic Nothing Might Explain Everything in the January 2024 issue of Scientific American depicts the entire Universe in a two-page spread — full of nothing.
The graphic uses the latest data from SDSS 12 and is an update to my Superclusters and Voids poster.
Michael Lemonick (editor) explains on the graphic:
“Regions of relatively empty space called cosmic voids are everywhere in the universe, and scientists believe studying their size, shape and spread across the cosmos could help them understand dark matter, dark energy and other big mysteries.
To use voids in this way, astronomers must map these regions in detail—a project that is just beginning.
Shown here are voids discovered by the Sloan Digital Sky Survey (SDSS), along with a selection of 16 previously named voids. Scientists expect voids to be evenly distributed throughout space—the lack of voids in some regions on the globe simply reflects SDSS’s sky coverage.”
voids
Sofia Contarini, Alice Pisani, Nico Hamaus, Federico Marulli Lauro Moscardini & Marco Baldi (2023) Cosmological Constraints from the BOSS DR12 Void Size Function Astrophysical Journal 953:46.
Nico Hamaus, Alice Pisani, Jin-Ah Choi, Guilhem Lavaux, Benjamin D. Wandelt & Jochen Weller (2020) Journal of Cosmology and Astroparticle Physics 2020:023.
Sloan Digital Sky Survey Data Release 12
Alan MacRobert (Sky & Telescope), Paulina Rowicka/Martin Krzywinski (revisions & Microscopium)
Hoffleit & Warren Jr. (1991) The Bright Star Catalog, 5th Revised Edition (Preliminary Version).
H0 = 67.4 km/(Mpc·s), Ωm = 0.315, Ωv = 0.685. Planck collaboration Planck 2018 results. VI. Cosmological parameters (2018).
constellation figures
stars
cosmology
Error in predictor variables
It is the mark of an educated mind to rest satisfied with the degree of precision that the nature of the subject admits and not to seek exactness where only an approximation is possible. —Aristotle
In regression, the predictors are (typically) assumed to have known values that are measured without error.
Practically, however, predictors are often measured with error. This has a profound (but predictable) effect on the estimates of relationships among variables – the so-called “error in variables” problem.
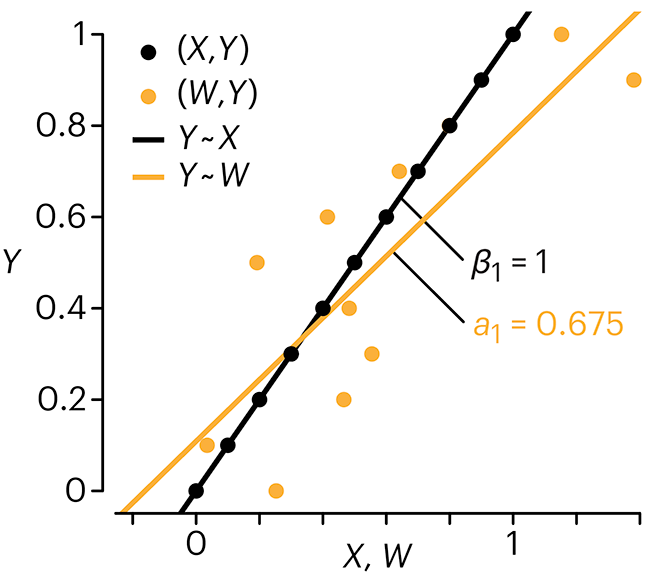
Error in measuring the predictors is often ignored. In this column, we discuss when ignoring this error is harmless and when it can lead to large bias that can leads us to miss important effects.
Altman, N. & Krzywinski, M. (2024) Points of significance: Error in predictor variables. Nat. Methods 20.
Background reading
Altman, N. & Krzywinski, M. (2015) Points of significance: Simple linear regression. Nat. Methods 12:999–1000.
Lever, J., Krzywinski, M. & Altman, N. (2016) Points of significance: Logistic regression. Nat. Methods 13:541–542 (2016).
Das, K., Krzywinski, M. & Altman, N. (2019) Points of significance: Quantile regression. Nat. Methods 16:451–452.
Convolutional neural networks
Nature uses only the longest threads to weave her patterns, so that each small piece of her fabric reveals the organization of the entire tapestry. – Richard Feynman
Following up on our Neural network primer column, this month we explore a different kind of network architecture: a convolutional network.
The convolutional network replaces the hidden layer of a fully connected network (FCN) with one or more filters (a kind of neuron that looks at the input within a narrow window).
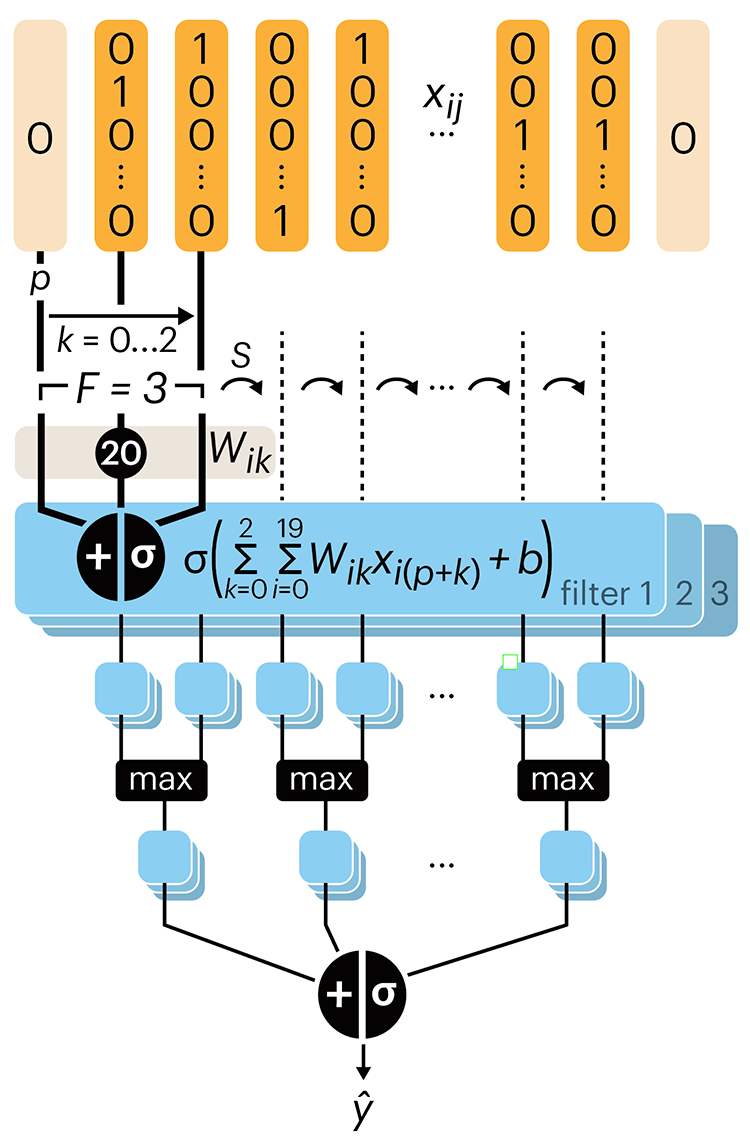
Even through convolutional networks have far fewer neurons that an FCN, they can perform substantially better for certain kinds of problems, such as sequence motif detection.
Derry, A., Krzywinski, M & Altman, N. (2023) Points of significance: Convolutional neural networks. Nature Methods 20:1269–1270.
Background reading
Derry, A., Krzywinski, M. & Altman, N. (2023) Points of significance: Neural network primer. Nature Methods 20:165–167.
Lever, J., Krzywinski, M. & Altman, N. (2016) Points of significance: Logistic regression. Nature Methods 13:541–542.