visualization + design
Haploid Genome Coverage Tables
Given a location `x` defined in the context of `h` chromosomes, the probability that position `x` is covered at least `\phi` times is `P_{h,\phi}` and given by $$ P_{h,\phi} = \left( 1 - \sum \frac{1}{k!} \left( \frac{\rho}{h}^k \right) e^{-\rho/h} \right)^h \tag{1} $$
For more details, see Wendl, M.C. and R.K. Wilson. 2008. Aspects of coverage in medical DNA sequencing. BMC Bioinformatics 9: 239.
For a given sequencing redundancy `\rho` (e.g. `\rho`-fold, as determined by the length of the haploid genome) of a haploid genome, the fraction of the haploid genome represented by at least `\phi` reads is reported by `P_{h,\phi}`. Coverage by fewer than `\phi` reads is reported as `1-P_{h,\phi}`. Coverage by exactly `\phi` reads is `P_{h,\phi} - P_{h,\phi+1}`. Entries for which fractional coverage is `\lt 10^{-5}` are not shown.
A rudimentary Monte Carlo simulation of genome coverage is also available, and is a useful supplement to the exact probabilities shown here.
http://mkweb.bcgsc.ca/coverage/?aneuploidy=12&depth=200
EXAMPLE 1
Suppose you carried out 3-fold redundant (`\rho=3`) sequencing of a haploid genome (`h=1`). 95.02% of the genome will be covered by at least one read (`P_{1,1}`) while 22.40% will be covered by exactly 3 reads (`P_{1,3} - P_{1,4}`).
EXAMPLE 2
You are sequencing a sample with a tumor content of 25% and you're interested in the depth of sequencing required to detect heterozygous mutations in the tumor. This scenario is equivalent to an aneuploidy = 8 genome—any given allele is present 8 times. If you sequence at (`\rho=200`), then 95% of the bases will be covered at a depth of at least `\phi = 14` (`P_{8,14} = 0.9494`). If you're satisfied with `\phi = 5` then you only need `\rho = 100` since now `P_{8,5} = 0.9580`.
ANALYTICAL vs STOCHASTIC
View plot that compares analytical vs stochastic results.
HAPLOID vs DIPLOID
View plot that compares 100x and 200x coverage of haploid and diploid genomes.
CODE
Download Perl scripts for analytical (to produce the tables below for any `\rho`) and stochastic coverage calculations.
sequencing redundancy for a haploid genome
View table for sequencing redundancy `\rho` = 1 2 3 4 5 6 7 8 9 10 20 25 50 75 100 of a haploid genome.
sequencing redundancy 1-fold (`\rho / h = 1.0`)
| `\phi` | `P_{h,\phi} - P_{h,\phi+1}` | `1-P_{h,\phi}` | `P_{h,\phi}` |
|---|---|---|---|
| 0 | 0.3679 | 0.0000 | 1.0000 |
| 1 | 0.3679 | 0.3679 | 0.6321 |
| 2 | 0.1839 | 0.7358 | 0.2642 |
| 3 | 0.0613 | 0.9197 | 0.0803 |
| 4 | 0.0153 | 0.9810 | 0.0190 |
| 5 | 0.0031 | 0.9963 | 0.0037 |
sequencing redundancy 2-fold (`\rho / h = 2.0`)
| `\phi` | `P_{h,\phi} - P_{h,\phi+1}` | `1-P_{h,\phi}` | `P_{h,\phi}` |
|---|---|---|---|
| 0 | 0.1353 | 0.0000 | 1.0000 |
| 1 | 0.2707 | 0.1353 | 0.8647 |
| 2 | 0.2707 | 0.4060 | 0.5940 |
| 3 | 0.1804 | 0.6767 | 0.3233 |
| 4 | 0.0902 | 0.8571 | 0.1429 |
| 5 | 0.0361 | 0.9473 | 0.0527 |
| 6 | 0.0120 | 0.9834 | 0.0166 |
| 7 | 0.0034 | 0.9955 | 0.0045 |
| 8 | 0.0009 | 0.9989 | 0.0011 |
| 9 | 0.0002 | 0.9998 | 0.0002 |
| 10 | 0.0000 | 1.0000 | 0.0000 |
sequencing redundancy 3-fold (`\rho / h = 3.0`)
| `\phi` | `P_{h,\phi} - P_{h,\phi+1}` | `1-P_{h,\phi}` | `P_{h,\phi}` |
|---|---|---|---|
| 0 | 0.0498 | 0.0000 | 1.0000 |
| 1 | 0.1494 | 0.0498 | 0.9502 |
| 2 | 0.2240 | 0.1991 | 0.8009 |
| 3 | 0.2240 | 0.4232 | 0.5768 |
| 4 | 0.1680 | 0.6472 | 0.3528 |
| 5 | 0.1008 | 0.8153 | 0.1847 |
| 6 | 0.0504 | 0.9161 | 0.0839 |
| 7 | 0.0216 | 0.9665 | 0.0335 |
| 8 | 0.0081 | 0.9881 | 0.0119 |
| 9 | 0.0027 | 0.9962 | 0.0038 |
| 10 | 0.0008 | 0.9989 | 0.0011 |
| 11 | 0.0002 | 0.9997 | 0.0003 |
| 12 | 0.0001 | 0.9999 | 0.0001 |
| 13 | 0.0000 | 1.0000 | 0.0000 |
sequencing redundancy 4-fold (`\rho / h = 4.0`)
| `\phi` | `P_{h,\phi} - P_{h,\phi+1}` | `1-P_{h,\phi}` | `P_{h,\phi}` |
|---|---|---|---|
| 0 | 0.0183 | 0.0000 | 1.0000 |
| 1 | 0.0733 | 0.0183 | 0.9817 |
| 2 | 0.1465 | 0.0916 | 0.9084 |
| 3 | 0.1954 | 0.2381 | 0.7619 |
| 4 | 0.1954 | 0.4335 | 0.5665 |
| 5 | 0.1563 | 0.6288 | 0.3712 |
| 6 | 0.1042 | 0.7851 | 0.2149 |
| 7 | 0.0595 | 0.8893 | 0.1107 |
| 8 | 0.0298 | 0.9489 | 0.0511 |
| 9 | 0.0132 | 0.9786 | 0.0214 |
| 10 | 0.0053 | 0.9919 | 0.0081 |
| 11 | 0.0019 | 0.9972 | 0.0028 |
| 12 | 0.0006 | 0.9991 | 0.0009 |
| 13 | 0.0002 | 0.9997 | 0.0003 |
| 14 | 0.0001 | 0.9999 | 0.0001 |
| 15 | 0.0000 | 1.0000 | 0.0000 |
sequencing redundancy 5-fold (`\rho / h = 5.0`)
| `\phi` | `P_{h,\phi} - P_{h,\phi+1}` | `1-P_{h,\phi}` | `P_{h,\phi}` |
|---|---|---|---|
| 0 | 0.0067 | 0.0000 | 1.0000 |
| 1 | 0.0337 | 0.0067 | 0.9933 |
| 2 | 0.0842 | 0.0404 | 0.9596 |
| 3 | 0.1404 | 0.1247 | 0.8753 |
| 4 | 0.1755 | 0.2650 | 0.7350 |
| 5 | 0.1755 | 0.4405 | 0.5595 |
| 6 | 0.1462 | 0.6160 | 0.3840 |
| 7 | 0.1044 | 0.7622 | 0.2378 |
| 8 | 0.0653 | 0.8666 | 0.1334 |
| 9 | 0.0363 | 0.9319 | 0.0681 |
| 10 | 0.0181 | 0.9682 | 0.0318 |
| 11 | 0.0082 | 0.9863 | 0.0137 |
| 12 | 0.0034 | 0.9945 | 0.0055 |
| 13 | 0.0013 | 0.9980 | 0.0020 |
| 14 | 0.0005 | 0.9993 | 0.0007 |
| 15 | 0.0002 | 0.9998 | 0.0002 |
| 16 | 0.0000 | 0.9999 | 0.0001 |
| 17 | 0.0000 | 1.0000 | 0.0000 |
sequencing redundancy 6-fold (`\rho / h = 6.0`)
| `\phi` | `P_{h,\phi} - P_{h,\phi+1}` | `1-P_{h,\phi}` | `P_{h,\phi}` |
|---|---|---|---|
| 0 | 0.0025 | 0.0000 | 1.0000 |
| 1 | 0.0149 | 0.0025 | 0.9975 |
| 2 | 0.0446 | 0.0174 | 0.9826 |
| 3 | 0.0892 | 0.0620 | 0.9380 |
| 4 | 0.1339 | 0.1512 | 0.8488 |
| 5 | 0.1606 | 0.2851 | 0.7149 |
| 6 | 0.1606 | 0.4457 | 0.5543 |
| 7 | 0.1377 | 0.6063 | 0.3937 |
| 8 | 0.1033 | 0.7440 | 0.2560 |
| 9 | 0.0688 | 0.8472 | 0.1528 |
| 10 | 0.0413 | 0.9161 | 0.0839 |
| 11 | 0.0225 | 0.9574 | 0.0426 |
| 12 | 0.0113 | 0.9799 | 0.0201 |
| 13 | 0.0052 | 0.9912 | 0.0088 |
| 14 | 0.0022 | 0.9964 | 0.0036 |
| 15 | 0.0009 | 0.9986 | 0.0014 |
| 16 | 0.0003 | 0.9995 | 0.0005 |
| 17 | 0.0001 | 0.9998 | 0.0002 |
| 18 | 0.0000 | 0.9999 | 0.0001 |
| 19 | 0.0000 | 1.0000 | 0.0000 |
sequencing redundancy 7-fold (`\rho / h = 7.0`)
| `\phi` | `P_{h,\phi} - P_{h,\phi+1}` | `1-P_{h,\phi}` | `P_{h,\phi}` |
|---|---|---|---|
| 0 | 0.0009 | 0.0000 | 1.0000 |
| 1 | 0.0064 | 0.0009 | 0.9991 |
| 2 | 0.0223 | 0.0073 | 0.9927 |
| 3 | 0.0521 | 0.0296 | 0.9704 |
| 4 | 0.0912 | 0.0818 | 0.9182 |
| 5 | 0.1277 | 0.1730 | 0.8270 |
| 6 | 0.1490 | 0.3007 | 0.6993 |
| 7 | 0.1490 | 0.4497 | 0.5503 |
| 8 | 0.1304 | 0.5987 | 0.4013 |
| 9 | 0.1014 | 0.7291 | 0.2709 |
| 10 | 0.0710 | 0.8305 | 0.1695 |
| 11 | 0.0452 | 0.9015 | 0.0985 |
| 12 | 0.0263 | 0.9467 | 0.0533 |
| 13 | 0.0142 | 0.9730 | 0.0270 |
| 14 | 0.0071 | 0.9872 | 0.0128 |
| 15 | 0.0033 | 0.9943 | 0.0057 |
| 16 | 0.0014 | 0.9976 | 0.0024 |
| 17 | 0.0006 | 0.9990 | 0.0010 |
| 18 | 0.0002 | 0.9996 | 0.0004 |
| 19 | 0.0001 | 0.9999 | 0.0001 |
| 20 | 0.0000 | 1.0000 | 0.0000 |
| 21 | 0.0000 | 1.0000 | 0.0000 |
sequencing redundancy 8-fold (`\rho / h = 8.0`)
| `\phi` | `P_{h,\phi} - P_{h,\phi+1}` | `1-P_{h,\phi}` | `P_{h,\phi}` |
|---|---|---|---|
| 0 | 0.0003 | 0.0000 | 1.0000 |
| 1 | 0.0027 | 0.0003 | 0.9997 |
| 2 | 0.0107 | 0.0030 | 0.9970 |
| 3 | 0.0286 | 0.0138 | 0.9862 |
| 4 | 0.0573 | 0.0424 | 0.9576 |
| 5 | 0.0916 | 0.0996 | 0.9004 |
| 6 | 0.1221 | 0.1912 | 0.8088 |
| 7 | 0.1396 | 0.3134 | 0.6866 |
| 8 | 0.1396 | 0.4530 | 0.5470 |
| 9 | 0.1241 | 0.5925 | 0.4075 |
| 10 | 0.0993 | 0.7166 | 0.2834 |
| 11 | 0.0722 | 0.8159 | 0.1841 |
| 12 | 0.0481 | 0.8881 | 0.1119 |
| 13 | 0.0296 | 0.9362 | 0.0638 |
| 14 | 0.0169 | 0.9658 | 0.0342 |
| 15 | 0.0090 | 0.9827 | 0.0173 |
| 16 | 0.0045 | 0.9918 | 0.0082 |
| 17 | 0.0021 | 0.9963 | 0.0037 |
| 18 | 0.0009 | 0.9984 | 0.0016 |
| 19 | 0.0004 | 0.9993 | 0.0007 |
| 20 | 0.0002 | 0.9997 | 0.0003 |
| 21 | 0.0001 | 0.9999 | 0.0001 |
| 22 | 0.0000 | 1.0000 | 0.0000 |
| 23 | 0.0000 | 1.0000 | 0.0000 |
sequencing redundancy 9-fold (`\rho / h = 9.0`)
| `\phi` | `P_{h,\phi} - P_{h,\phi+1}` | `1-P_{h,\phi}` | `P_{h,\phi}` |
|---|---|---|---|
| 0 | 0.0001 | 0.0000 | 1.0000 |
| 1 | 0.0011 | 0.0001 | 0.9999 |
| 2 | 0.0050 | 0.0012 | 0.9988 |
| 3 | 0.0150 | 0.0062 | 0.9938 |
| 4 | 0.0337 | 0.0212 | 0.9788 |
| 5 | 0.0607 | 0.0550 | 0.9450 |
| 6 | 0.0911 | 0.1157 | 0.8843 |
| 7 | 0.1171 | 0.2068 | 0.7932 |
| 8 | 0.1318 | 0.3239 | 0.6761 |
| 9 | 0.1318 | 0.4557 | 0.5443 |
| 10 | 0.1186 | 0.5874 | 0.4126 |
| 11 | 0.0970 | 0.7060 | 0.2940 |
| 12 | 0.0728 | 0.8030 | 0.1970 |
| 13 | 0.0504 | 0.8758 | 0.1242 |
| 14 | 0.0324 | 0.9261 | 0.0739 |
| 15 | 0.0194 | 0.9585 | 0.0415 |
| 16 | 0.0109 | 0.9780 | 0.0220 |
| 17 | 0.0058 | 0.9889 | 0.0111 |
| 18 | 0.0029 | 0.9947 | 0.0053 |
| 19 | 0.0014 | 0.9976 | 0.0024 |
| 20 | 0.0006 | 0.9989 | 0.0011 |
| 21 | 0.0003 | 0.9996 | 0.0004 |
| 22 | 0.0001 | 0.9998 | 0.0002 |
| 23 | 0.0000 | 0.9999 | 0.0001 |
| 24 | 0.0000 | 1.0000 | 0.0000 |
sequencing redundancy 10-fold (`\rho / h = 10.0`)
| `\phi` | `P_{h,\phi} - P_{h,\phi+1}` | `1-P_{h,\phi}` | `P_{h,\phi}` |
|---|---|---|---|
| 0 | 0.0000 | 0.0000 | 1.0000 |
| 1 | 0.0005 | 0.0000 | 1.0000 |
| 2 | 0.0023 | 0.0005 | 0.9995 |
| 3 | 0.0076 | 0.0028 | 0.9972 |
| 4 | 0.0189 | 0.0103 | 0.9897 |
| 5 | 0.0378 | 0.0293 | 0.9707 |
| 6 | 0.0631 | 0.0671 | 0.9329 |
| 7 | 0.0901 | 0.1301 | 0.8699 |
| 8 | 0.1126 | 0.2202 | 0.7798 |
| 9 | 0.1251 | 0.3328 | 0.6672 |
| 10 | 0.1251 | 0.4579 | 0.5421 |
| 11 | 0.1137 | 0.5830 | 0.4170 |
| 12 | 0.0948 | 0.6968 | 0.3032 |
| 13 | 0.0729 | 0.7916 | 0.2084 |
| 14 | 0.0521 | 0.8645 | 0.1355 |
| 15 | 0.0347 | 0.9165 | 0.0835 |
| 16 | 0.0217 | 0.9513 | 0.0487 |
| 17 | 0.0128 | 0.9730 | 0.0270 |
| 18 | 0.0071 | 0.9857 | 0.0143 |
| 19 | 0.0037 | 0.9928 | 0.0072 |
| 20 | 0.0019 | 0.9965 | 0.0035 |
| 21 | 0.0009 | 0.9984 | 0.0016 |
| 22 | 0.0004 | 0.9993 | 0.0007 |
| 23 | 0.0002 | 0.9997 | 0.0003 |
| 24 | 0.0001 | 0.9999 | 0.0001 |
| 25 | 0.0000 | 1.0000 | 0.0000 |
| 26 | 0.0000 | 1.0000 | 0.0000 |
sequencing redundancy 20-fold (`\rho / h = 20.0`)
| `\phi` | `P_{h,\phi} - P_{h,\phi+1}` | `1-P_{h,\phi}` | `P_{h,\phi}` |
|---|---|---|---|
| 4 | 0.0000 | 0.0000 | 1.0000 |
| 5 | 0.0001 | 0.0000 | 1.0000 |
| 6 | 0.0002 | 0.0001 | 0.9999 |
| 7 | 0.0005 | 0.0003 | 0.9997 |
| 8 | 0.0013 | 0.0008 | 0.9992 |
| 9 | 0.0029 | 0.0021 | 0.9979 |
| 10 | 0.0058 | 0.0050 | 0.9950 |
| 11 | 0.0106 | 0.0108 | 0.9892 |
| 12 | 0.0176 | 0.0214 | 0.9786 |
| 13 | 0.0271 | 0.0390 | 0.9610 |
| 14 | 0.0387 | 0.0661 | 0.9339 |
| 15 | 0.0516 | 0.1049 | 0.8951 |
| 16 | 0.0646 | 0.1565 | 0.8435 |
| 17 | 0.0760 | 0.2211 | 0.7789 |
| 18 | 0.0844 | 0.2970 | 0.7030 |
| 19 | 0.0888 | 0.3814 | 0.6186 |
| 20 | 0.0888 | 0.4703 | 0.5297 |
| 21 | 0.0846 | 0.5591 | 0.4409 |
| 22 | 0.0769 | 0.6437 | 0.3563 |
| 23 | 0.0669 | 0.7206 | 0.2794 |
| 24 | 0.0557 | 0.7875 | 0.2125 |
| 25 | 0.0446 | 0.8432 | 0.1568 |
| 26 | 0.0343 | 0.8878 | 0.1122 |
| 27 | 0.0254 | 0.9221 | 0.0779 |
| 28 | 0.0181 | 0.9475 | 0.0525 |
| 29 | 0.0125 | 0.9657 | 0.0343 |
| 30 | 0.0083 | 0.9782 | 0.0218 |
| 31 | 0.0054 | 0.9865 | 0.0135 |
| 32 | 0.0034 | 0.9919 | 0.0081 |
| 33 | 0.0020 | 0.9953 | 0.0047 |
| 34 | 0.0012 | 0.9973 | 0.0027 |
| 35 | 0.0007 | 0.9985 | 0.0015 |
| 36 | 0.0004 | 0.9992 | 0.0008 |
| 37 | 0.0002 | 0.9996 | 0.0004 |
| 38 | 0.0001 | 0.9998 | 0.0002 |
| 39 | 0.0001 | 0.9999 | 0.0001 |
| 40 | 0.0000 | 0.9999 | 0.0001 |
| 41 | 0.0000 | 1.0000 | 0.0000 |
| 42 | 0.0000 | 1.0000 | 0.0000 |
sequencing redundancy 25-fold (`\rho / h = 25.0`)
| `\phi` | `P_{h,\phi} - P_{h,\phi+1}` | `1-P_{h,\phi}` | `P_{h,\phi}` |
|---|---|---|---|
| 7 | 0.0000 | 0.0000 | 1.0000 |
| 8 | 0.0001 | 0.0000 | 1.0000 |
| 9 | 0.0001 | 0.0001 | 0.9999 |
| 10 | 0.0004 | 0.0002 | 0.9998 |
| 11 | 0.0008 | 0.0006 | 0.9994 |
| 12 | 0.0017 | 0.0014 | 0.9986 |
| 13 | 0.0033 | 0.0031 | 0.9969 |
| 14 | 0.0059 | 0.0065 | 0.9935 |
| 15 | 0.0099 | 0.0124 | 0.9876 |
| 16 | 0.0155 | 0.0223 | 0.9777 |
| 17 | 0.0227 | 0.0377 | 0.9623 |
| 18 | 0.0316 | 0.0605 | 0.9395 |
| 19 | 0.0415 | 0.0920 | 0.9080 |
| 20 | 0.0519 | 0.1336 | 0.8664 |
| 21 | 0.0618 | 0.1855 | 0.8145 |
| 22 | 0.0702 | 0.2473 | 0.7527 |
| 23 | 0.0763 | 0.3175 | 0.6825 |
| 24 | 0.0795 | 0.3939 | 0.6061 |
| 25 | 0.0795 | 0.4734 | 0.5266 |
| 26 | 0.0765 | 0.5529 | 0.4471 |
| 27 | 0.0708 | 0.6294 | 0.3706 |
| 28 | 0.0632 | 0.7002 | 0.2998 |
| 29 | 0.0545 | 0.7634 | 0.2366 |
| 30 | 0.0454 | 0.8179 | 0.1821 |
| 31 | 0.0366 | 0.8633 | 0.1367 |
| 32 | 0.0286 | 0.8999 | 0.1001 |
| 33 | 0.0217 | 0.9285 | 0.0715 |
| 34 | 0.0159 | 0.9502 | 0.0498 |
| 35 | 0.0114 | 0.9662 | 0.0338 |
| 36 | 0.0079 | 0.9775 | 0.0225 |
| 37 | 0.0053 | 0.9854 | 0.0146 |
| 38 | 0.0035 | 0.9908 | 0.0092 |
| 39 | 0.0023 | 0.9943 | 0.0057 |
| 40 | 0.0014 | 0.9966 | 0.0034 |
| 41 | 0.0009 | 0.9980 | 0.0020 |
| 42 | 0.0005 | 0.9988 | 0.0012 |
| 43 | 0.0003 | 0.9993 | 0.0007 |
| 44 | 0.0002 | 0.9996 | 0.0004 |
| 45 | 0.0001 | 0.9998 | 0.0002 |
| 46 | 0.0001 | 0.9999 | 0.0001 |
| 47 | 0.0000 | 0.9999 | 0.0001 |
| 48 | 0.0000 | 1.0000 | 0.0000 |
| 49 | 0.0000 | 1.0000 | 0.0000 |
sequencing redundancy 50-fold (`\rho / h = 50.0`)
| `\phi` | `P_{h,\phi} - P_{h,\phi+1}` | `1-P_{h,\phi}` | `P_{h,\phi}` |
|---|---|---|---|
| 24 | 0.0000 | 0.0000 | 1.0000 |
| 25 | 0.0000 | 0.0000 | 1.0000 |
| 26 | 0.0001 | 0.0001 | 0.9999 |
| 27 | 0.0001 | 0.0001 | 0.9999 |
| 28 | 0.0002 | 0.0003 | 0.9997 |
| 29 | 0.0004 | 0.0005 | 0.9995 |
| 30 | 0.0007 | 0.0009 | 0.9991 |
| 31 | 0.0011 | 0.0016 | 0.9984 |
| 32 | 0.0017 | 0.0027 | 0.9973 |
| 33 | 0.0026 | 0.0044 | 0.9956 |
| 34 | 0.0038 | 0.0070 | 0.9930 |
| 35 | 0.0054 | 0.0108 | 0.9892 |
| 36 | 0.0075 | 0.0162 | 0.9838 |
| 37 | 0.0102 | 0.0238 | 0.9762 |
| 38 | 0.0134 | 0.0340 | 0.9660 |
| 39 | 0.0172 | 0.0474 | 0.9526 |
| 40 | 0.0215 | 0.0646 | 0.9354 |
| 41 | 0.0262 | 0.0861 | 0.9139 |
| 42 | 0.0312 | 0.1123 | 0.8877 |
| 43 | 0.0363 | 0.1435 | 0.8565 |
| 44 | 0.0412 | 0.1798 | 0.8202 |
| 45 | 0.0458 | 0.2210 | 0.7790 |
| 46 | 0.0498 | 0.2669 | 0.7331 |
| 47 | 0.0530 | 0.3167 | 0.6833 |
| 48 | 0.0552 | 0.3697 | 0.6303 |
| 49 | 0.0563 | 0.4249 | 0.5751 |
| 50 | 0.0563 | 0.4812 | 0.5188 |
| 51 | 0.0552 | 0.5375 | 0.4625 |
| 52 | 0.0531 | 0.5927 | 0.4073 |
| 53 | 0.0501 | 0.6458 | 0.3542 |
| 54 | 0.0464 | 0.6959 | 0.3041 |
| 55 | 0.0422 | 0.7423 | 0.2577 |
| 56 | 0.0376 | 0.7845 | 0.2155 |
| 57 | 0.0330 | 0.8221 | 0.1779 |
| 58 | 0.0285 | 0.8551 | 0.1449 |
| 59 | 0.0241 | 0.8836 | 0.1164 |
| 60 | 0.0201 | 0.9077 | 0.0923 |
| 61 | 0.0165 | 0.9278 | 0.0722 |
| 62 | 0.0133 | 0.9443 | 0.0557 |
| 63 | 0.0105 | 0.9576 | 0.0424 |
| 64 | 0.0082 | 0.9682 | 0.0318 |
| 65 | 0.0063 | 0.9764 | 0.0236 |
| 66 | 0.0048 | 0.9827 | 0.0173 |
| 67 | 0.0036 | 0.9875 | 0.0125 |
| 68 | 0.0026 | 0.9911 | 0.0089 |
| 69 | 0.0019 | 0.9938 | 0.0062 |
| 70 | 0.0014 | 0.9957 | 0.0043 |
| 71 | 0.0010 | 0.9970 | 0.0030 |
| 72 | 0.0007 | 0.9980 | 0.0020 |
| 73 | 0.0005 | 0.9987 | 0.0013 |
| 74 | 0.0003 | 0.9991 | 0.0009 |
| 75 | 0.0002 | 0.9994 | 0.0006 |
| 76 | 0.0001 | 0.9996 | 0.0004 |
| 77 | 0.0001 | 0.9998 | 0.0002 |
| 78 | 0.0001 | 0.9999 | 0.0001 |
| 79 | 0.0000 | 0.9999 | 0.0001 |
| 80 | 0.0000 | 0.9999 | 0.0001 |
| 81 | 0.0000 | 1.0000 | 0.0000 |
| 82 | 0.0000 | 1.0000 | 0.0000 |
| 83 | 0.0000 | 1.0000 | 0.0000 |
sequencing redundancy 75-fold (`\rho / h = 75.0`)
| `\phi` | `P_{h,\phi} - P_{h,\phi+1}` | `1-P_{h,\phi}` | `P_{h,\phi}` |
|---|---|---|---|
| 42 | 0.0000 | 0.0000 | 1.0000 |
| 43 | 0.0000 | 0.0000 | 1.0000 |
| 44 | 0.0000 | 0.0000 | 1.0000 |
| 45 | 0.0001 | 0.0001 | 0.9999 |
| 46 | 0.0001 | 0.0001 | 0.9999 |
| 47 | 0.0001 | 0.0002 | 0.9998 |
| 48 | 0.0002 | 0.0004 | 0.9996 |
| 49 | 0.0003 | 0.0006 | 0.9994 |
| 50 | 0.0005 | 0.0009 | 0.9991 |
| 51 | 0.0007 | 0.0014 | 0.9986 |
| 52 | 0.0011 | 0.0021 | 0.9979 |
| 53 | 0.0015 | 0.0032 | 0.9968 |
| 54 | 0.0021 | 0.0047 | 0.9953 |
| 55 | 0.0028 | 0.0068 | 0.9932 |
| 56 | 0.0038 | 0.0096 | 0.9904 |
| 57 | 0.0050 | 0.0134 | 0.9866 |
| 58 | 0.0065 | 0.0184 | 0.9816 |
| 59 | 0.0082 | 0.0249 | 0.9751 |
| 60 | 0.0103 | 0.0331 | 0.9669 |
| 61 | 0.0126 | 0.0433 | 0.9567 |
| 62 | 0.0153 | 0.0560 | 0.9440 |
| 63 | 0.0182 | 0.0712 | 0.9288 |
| 64 | 0.0213 | 0.0894 | 0.9106 |
| 65 | 0.0246 | 0.1107 | 0.8893 |
| 66 | 0.0279 | 0.1353 | 0.8647 |
| 67 | 0.0313 | 0.1632 | 0.8368 |
| 68 | 0.0345 | 0.1945 | 0.8055 |
| 69 | 0.0375 | 0.2290 | 0.7710 |
| 70 | 0.0402 | 0.2665 | 0.7335 |
| 71 | 0.0424 | 0.3066 | 0.6934 |
| 72 | 0.0442 | 0.3490 | 0.6510 |
| 73 | 0.0454 | 0.3932 | 0.6068 |
| 74 | 0.0460 | 0.4386 | 0.5614 |
| 75 | 0.0460 | 0.4846 | 0.5154 |
| 76 | 0.0454 | 0.5307 | 0.4693 |
| 77 | 0.0442 | 0.5761 | 0.4239 |
| 78 | 0.0425 | 0.6203 | 0.3797 |
| 79 | 0.0404 | 0.6628 | 0.3372 |
| 80 | 0.0379 | 0.7032 | 0.2968 |
| 81 | 0.0350 | 0.7411 | 0.2589 |
| 82 | 0.0321 | 0.7761 | 0.2239 |
| 83 | 0.0290 | 0.8082 | 0.1918 |
| 84 | 0.0259 | 0.8371 | 0.1629 |
| 85 | 0.0228 | 0.8630 | 0.1370 |
| 86 | 0.0199 | 0.8858 | 0.1142 |
| 87 | 0.0172 | 0.9057 | 0.0943 |
| 88 | 0.0146 | 0.9229 | 0.0771 |
| 89 | 0.0123 | 0.9375 | 0.0625 |
| 90 | 0.0103 | 0.9498 | 0.0502 |
| 91 | 0.0085 | 0.9601 | 0.0399 |
| 92 | 0.0069 | 0.9685 | 0.0315 |
| 93 | 0.0056 | 0.9754 | 0.0246 |
| 94 | 0.0044 | 0.9810 | 0.0190 |
| 95 | 0.0035 | 0.9854 | 0.0146 |
| 96 | 0.0027 | 0.9889 | 0.0111 |
| 97 | 0.0021 | 0.9917 | 0.0083 |
| 98 | 0.0016 | 0.9938 | 0.0062 |
| 99 | 0.0012 | 0.9954 | 0.0046 |
| 100 | 0.0009 | 0.9966 | 0.0034 |
| 101 | 0.0007 | 0.9976 | 0.0024 |
| 102 | 0.0005 | 0.9983 | 0.0017 |
| 103 | 0.0004 | 0.9988 | 0.0012 |
| 104 | 0.0003 | 0.9991 | 0.0009 |
| 105 | 0.0002 | 0.9994 | 0.0006 |
| 106 | 0.0001 | 0.9996 | 0.0004 |
| 107 | 0.0001 | 0.9997 | 0.0003 |
| 108 | 0.0001 | 0.9998 | 0.0002 |
| 109 | 0.0000 | 0.9999 | 0.0001 |
| 110 | 0.0000 | 0.9999 | 0.0001 |
| 111 | 0.0000 | 0.9999 | 0.0001 |
| 112 | 0.0000 | 1.0000 | 0.0000 |
| 113 | 0.0000 | 1.0000 | 0.0000 |
| 114 | 0.0000 | 1.0000 | 0.0000 |
| 115 | 0.0000 | 1.0000 | 0.0000 |
sequencing redundancy 100-fold (`\rho / h = 100.0`)
| `\phi` | `P_{h,\phi} - P_{h,\phi+1}` | `1-P_{h,\phi}` | `P_{h,\phi}` |
|---|---|---|---|
| 61 | 0.0000 | 0.0000 | 1.0000 |
| 62 | 0.0000 | 0.0000 | 1.0000 |
| 63 | 0.0000 | 0.0000 | 1.0000 |
| 64 | 0.0000 | 0.0000 | 1.0000 |
| 65 | 0.0000 | 0.0001 | 0.9999 |
| 66 | 0.0001 | 0.0001 | 0.9999 |
| 67 | 0.0001 | 0.0002 | 0.9998 |
| 68 | 0.0002 | 0.0003 | 0.9997 |
| 69 | 0.0002 | 0.0004 | 0.9996 |
| 70 | 0.0003 | 0.0007 | 0.9993 |
| 71 | 0.0004 | 0.0010 | 0.9990 |
| 72 | 0.0006 | 0.0014 | 0.9986 |
| 73 | 0.0008 | 0.0020 | 0.9980 |
| 74 | 0.0011 | 0.0028 | 0.9972 |
| 75 | 0.0015 | 0.0040 | 0.9960 |
| 76 | 0.0020 | 0.0055 | 0.9945 |
| 77 | 0.0026 | 0.0074 | 0.9926 |
| 78 | 0.0033 | 0.0100 | 0.9900 |
| 79 | 0.0042 | 0.0133 | 0.9867 |
| 80 | 0.0052 | 0.0175 | 0.9825 |
| 81 | 0.0064 | 0.0226 | 0.9774 |
| 82 | 0.0078 | 0.0291 | 0.9709 |
| 83 | 0.0094 | 0.0369 | 0.9631 |
| 84 | 0.0112 | 0.0463 | 0.9537 |
| 85 | 0.0132 | 0.0575 | 0.9425 |
| 86 | 0.0154 | 0.0708 | 0.9292 |
| 87 | 0.0176 | 0.0861 | 0.9139 |
| 88 | 0.0201 | 0.1038 | 0.8962 |
| 89 | 0.0225 | 0.1238 | 0.8762 |
| 90 | 0.0250 | 0.1463 | 0.8537 |
| 91 | 0.0275 | 0.1714 | 0.8286 |
| 92 | 0.0299 | 0.1989 | 0.8011 |
| 93 | 0.0322 | 0.2288 | 0.7712 |
| 94 | 0.0342 | 0.2610 | 0.7390 |
| 95 | 0.0360 | 0.2952 | 0.7048 |
| 96 | 0.0375 | 0.3312 | 0.6688 |
| 97 | 0.0387 | 0.3687 | 0.6313 |
| 98 | 0.0395 | 0.4074 | 0.5926 |
| 99 | 0.0399 | 0.4468 | 0.5532 |
| 100 | 0.0399 | 0.4867 | 0.5133 |
| 101 | 0.0395 | 0.5266 | 0.4734 |
| 102 | 0.0387 | 0.5660 | 0.4340 |
| 103 | 0.0376 | 0.6047 | 0.3953 |
| 104 | 0.0361 | 0.6423 | 0.3577 |
| 105 | 0.0344 | 0.6784 | 0.3216 |
| 106 | 0.0325 | 0.7128 | 0.2872 |
| 107 | 0.0303 | 0.7453 | 0.2547 |
| 108 | 0.0281 | 0.7756 | 0.2244 |
| 109 | 0.0258 | 0.8037 | 0.1963 |
| 110 | 0.0234 | 0.8294 | 0.1706 |
| 111 | 0.0211 | 0.8529 | 0.1471 |
| 112 | 0.0188 | 0.8740 | 0.1260 |
| 113 | 0.0167 | 0.8928 | 0.1072 |
| 114 | 0.0146 | 0.9095 | 0.0905 |
| 115 | 0.0127 | 0.9241 | 0.0759 |
| 116 | 0.0110 | 0.9368 | 0.0632 |
| 117 | 0.0094 | 0.9478 | 0.0522 |
| 118 | 0.0079 | 0.9572 | 0.0428 |
| 119 | 0.0067 | 0.9651 | 0.0349 |
| 120 | 0.0056 | 0.9718 | 0.0282 |
| 121 | 0.0046 | 0.9773 | 0.0227 |
| 122 | 0.0038 | 0.9819 | 0.0181 |
| 123 | 0.0031 | 0.9857 | 0.0143 |
| 124 | 0.0025 | 0.9888 | 0.0112 |
| 125 | 0.0020 | 0.9912 | 0.0088 |
| 126 | 0.0016 | 0.9932 | 0.0068 |
| 127 | 0.0012 | 0.9948 | 0.0052 |
| 128 | 0.0010 | 0.9960 | 0.0040 |
| 129 | 0.0007 | 0.9970 | 0.0030 |
| 130 | 0.0006 | 0.9977 | 0.0023 |
| 131 | 0.0004 | 0.9983 | 0.0017 |
| 132 | 0.0003 | 0.9987 | 0.0013 |
| 133 | 0.0003 | 0.9991 | 0.0009 |
| 134 | 0.0002 | 0.9993 | 0.0007 |
| 135 | 0.0001 | 0.9995 | 0.0005 |
| 136 | 0.0001 | 0.9996 | 0.0004 |
| 137 | 0.0001 | 0.9997 | 0.0003 |
| 138 | 0.0001 | 0.9998 | 0.0002 |
| 139 | 0.0000 | 0.9999 | 0.0001 |
| 140 | 0.0000 | 0.9999 | 0.0001 |
| 141 | 0.0000 | 0.9999 | 0.0001 |
| 142 | 0.0000 | 1.0000 | 0.0000 |
| 143 | 0.0000 | 1.0000 | 0.0000 |
| 144 | 0.0000 | 1.0000 | 0.0000 |
| 145 | 0.0000 | 1.0000 | 0.0000 |
Nasa to send our human genome discs to the Moon
We'd like to say a ‘cosmic hello’: mathematics, culture, palaeontology, art and science, and ... human genomes.



Comparing classifier performance with baselines
All animals are equal, but some animals are more equal than others. —George Orwell
This month, we will illustrate the importance of establishing a baseline performance level.
Baselines are typically generated independently for each dataset using very simple models. Their role is to set the minimum level of acceptable performance and help with comparing relative improvements in performance of other models.
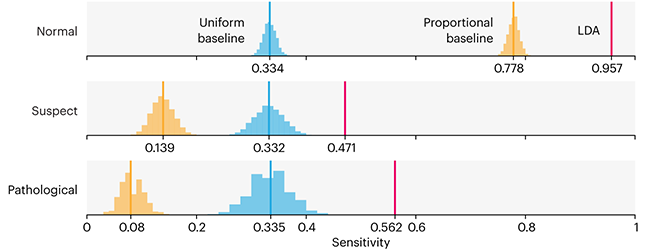
Unfortunately, baselines are often overlooked and, in the presence of a class imbalance5, must be established with care.
Megahed, F.M, Chen, Y-J., Jones-Farmer, A., Rigdon, S.E., Krzywinski, M. & Altman, N. (2024) Points of significance: Comparing classifier performance with baselines. Nat. Methods 20.
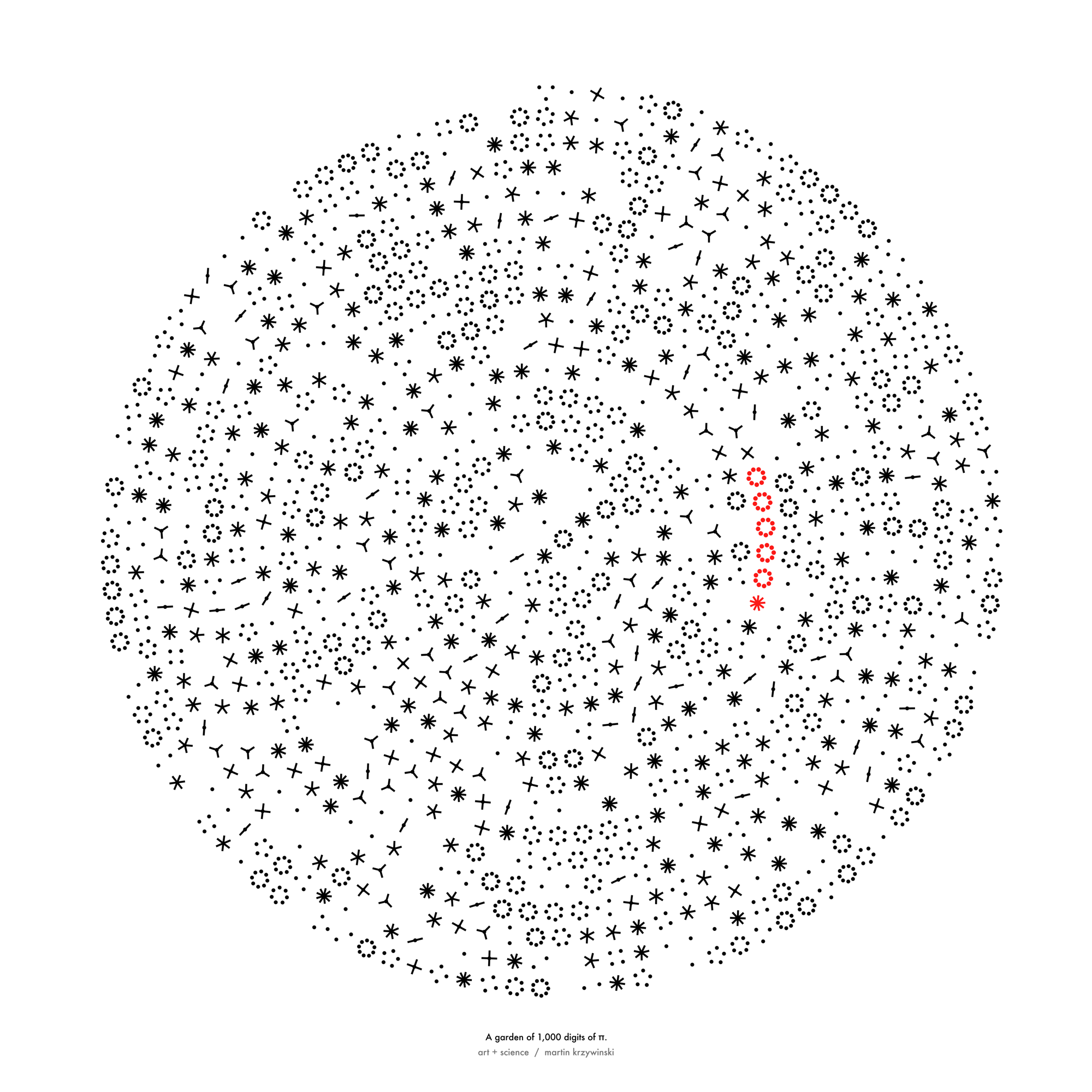
Happy 2024 π Day—
sunflowers ho!
Celebrate π Day (March 14th) and dig into the digit garden. Let's grow something.
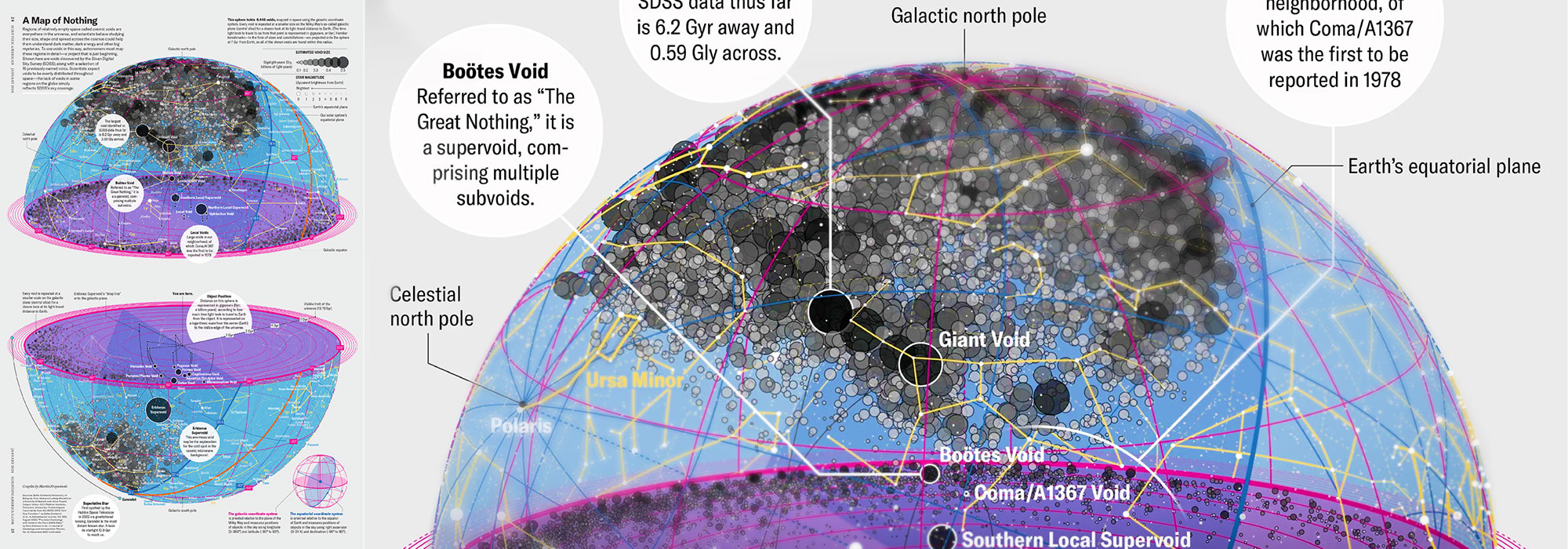
How Analyzing Cosmic Nothing Might Explain Everything
Huge empty areas of the universe called voids could help solve the greatest mysteries in the cosmos.
My graphic accompanying How Analyzing Cosmic Nothing Might Explain Everything in the January 2024 issue of Scientific American depicts the entire Universe in a two-page spread — full of nothing.
The graphic uses the latest data from SDSS 12 and is an update to my Superclusters and Voids poster.
Michael Lemonick (editor) explains on the graphic:
“Regions of relatively empty space called cosmic voids are everywhere in the universe, and scientists believe studying their size, shape and spread across the cosmos could help them understand dark matter, dark energy and other big mysteries.
To use voids in this way, astronomers must map these regions in detail—a project that is just beginning.
Shown here are voids discovered by the Sloan Digital Sky Survey (SDSS), along with a selection of 16 previously named voids. Scientists expect voids to be evenly distributed throughout space—the lack of voids in some regions on the globe simply reflects SDSS’s sky coverage.”
voids
Sofia Contarini, Alice Pisani, Nico Hamaus, Federico Marulli Lauro Moscardini & Marco Baldi (2023) Cosmological Constraints from the BOSS DR12 Void Size Function Astrophysical Journal 953:46.
Nico Hamaus, Alice Pisani, Jin-Ah Choi, Guilhem Lavaux, Benjamin D. Wandelt & Jochen Weller (2020) Journal of Cosmology and Astroparticle Physics 2020:023.
Sloan Digital Sky Survey Data Release 12
Alan MacRobert (Sky & Telescope), Paulina Rowicka/Martin Krzywinski (revisions & Microscopium)
Hoffleit & Warren Jr. (1991) The Bright Star Catalog, 5th Revised Edition (Preliminary Version).
H0 = 67.4 km/(Mpc·s), Ωm = 0.315, Ωv = 0.685. Planck collaboration Planck 2018 results. VI. Cosmological parameters (2018).
constellation figures
stars
cosmology
Error in predictor variables
It is the mark of an educated mind to rest satisfied with the degree of precision that the nature of the subject admits and not to seek exactness where only an approximation is possible. —Aristotle
In regression, the predictors are (typically) assumed to have known values that are measured without error.
Practically, however, predictors are often measured with error. This has a profound (but predictable) effect on the estimates of relationships among variables – the so-called “error in variables” problem.
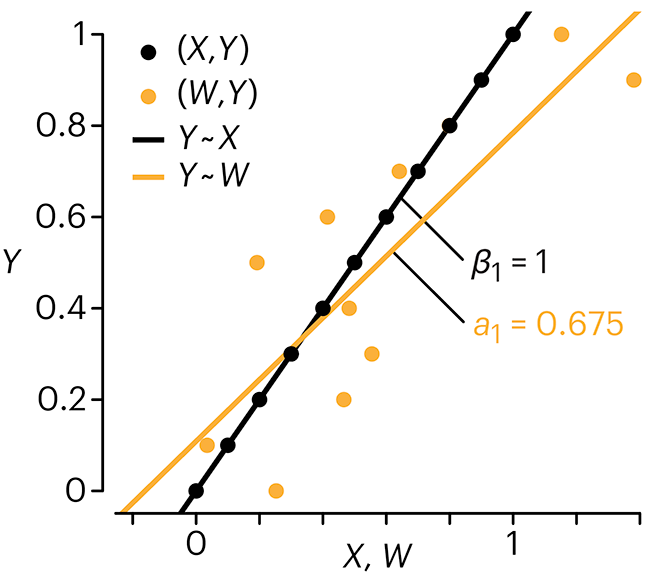
Error in measuring the predictors is often ignored. In this column, we discuss when ignoring this error is harmless and when it can lead to large bias that can leads us to miss important effects.
Altman, N. & Krzywinski, M. (2024) Points of significance: Error in predictor variables. Nat. Methods 20.
Background reading
Altman, N. & Krzywinski, M. (2015) Points of significance: Simple linear regression. Nat. Methods 12:999–1000.
Lever, J., Krzywinski, M. & Altman, N. (2016) Points of significance: Logistic regression. Nat. Methods 13:541–542 (2016).
Das, K., Krzywinski, M. & Altman, N. (2019) Points of significance: Quantile regression. Nat. Methods 16:451–452.
Convolutional neural networks
Nature uses only the longest threads to weave her patterns, so that each small piece of her fabric reveals the organization of the entire tapestry. – Richard Feynman
Following up on our Neural network primer column, this month we explore a different kind of network architecture: a convolutional network.
The convolutional network replaces the hidden layer of a fully connected network (FCN) with one or more filters (a kind of neuron that looks at the input within a narrow window).
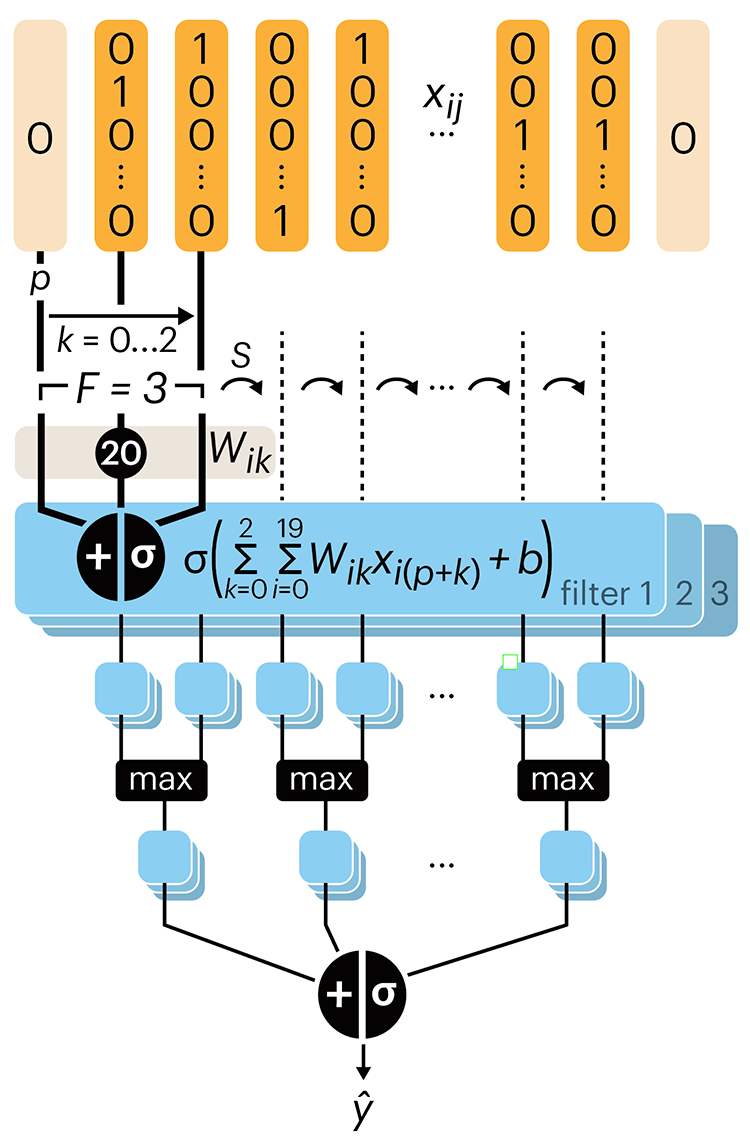
Even through convolutional networks have far fewer neurons that an FCN, they can perform substantially better for certain kinds of problems, such as sequence motif detection.
Derry, A., Krzywinski, M & Altman, N. (2023) Points of significance: Convolutional neural networks. Nature Methods 20:1269–1270.
Background reading
Derry, A., Krzywinski, M. & Altman, N. (2023) Points of significance: Neural network primer. Nature Methods 20:165–167.
Lever, J., Krzywinski, M. & Altman, N. (2016) Points of significance: Logistic regression. Nature Methods 13:541–542.